피지여행 3번째 논문

논문 저자 : Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver & Daan Wierstra
논문 링크 : https://arxiv.org/pdf/1509.02971.pdf
Proceeding : International Conference on Learning Representations (ICLR) 2016
정리 : 양혁렬, 이동민, 차금강
1. 들어가며...
1.1 Success & Limitation of DQN
- Success
- sensor로부터 나오는 전처리를 거친 input 대신에 raw pixel input을 사용합니다. 이렇게 함으로써 High dimensional observation space 문제를 풀어냅니다.
- Limitation
- discrete & low dimensional action space만 다룰 수 있습니다. Continuous action space를 다루기 위해서는 매 스텝 이를 위한 iterative optimization process를 거쳐야 합니다.
1.2 Problems of discretization

- 만약 7개의 관절을 가진 로봇 팔이 있다면, 가장 간단한 discretization은 각 관절을 다음과 같이 $a_{i}\in { -k, 0, k \\}$ 3개의 값을 가지도록 하는 것입니다.
- 그렇다면 $3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 3^{7} = 2187$ 가지의 dimension을 가진 action space가 만들어집니다. 이와같이 Discretization을 하면 action space가 exponential하게 늘어납니다.
- 충분히 큰 action space 임에도 discretization으로 인한 정보의 손실이 있을 수 있고, 섬세한 Control을 할 수 없습니다.
1.3 New approach for continuous control
- Model-free, Off-policy, Actor-critic algorithm을 제안합니다.
- Deep Deterministic Policy(이하 DPG)를 기반으로 합니다.
- Actor-Critic approach와 DQN의 성공적이었던 부분을 합칩니다.
- Replay buffer : 샘플들 사이의 상관관계를 줄여줍니다.
- target Q Network : Update 동안 target을 안정적으로 만듭니다.
2. Background
2.1 Notation
- Observation : $x_{t}$
- Action : $a_t \in {\rm IR}^N$
- Reward : $r_t$
- Discount factor : $\gamma$
- Environment : $E$
- Policy : $\pi : S \rightarrow P(A)$
- Transition dynamics : $p(s_{t+1} \vert s_t, a_t)$
- Reward function : $r(s_t, a_t)$
- Return : $\sum_{ i=t }^{ T } \gamma^{(i-t)}r(s_i, a_i)$
- Discounted state visitation distribution for a policy : $\rho^\pi$
2.2 Bellman Equation
- 상태 $s_t$에서 행동 $a_t$를 취했을 때 Expected return은 다음과 같습니다.
$$ Q^{\pi}(s_t, a_t)={\rm E}{r{i \geqq t},s_{i \geqq t} \backsim E, a_{i \geqq t} \backsim \pi } [R_{t} \vert s_t, a_t ] $$
- 벨만 방정식을 사용하여 위의 식을 변형합니다.
$$ Q^{\pi}(s_t, a_t)={\rm E}_{r_{t},s_{t} \backsim E} [r(s_t,a_t)+\gamma {\rm E}_{a_{t+1} \backsim \pi } [ Q^{\pi}(s_{t+1}, a_{t+1}) ] ] $$
- Determinsitc policy를 가정합니다.
$$ Q^{\mu}(s_t, a_t)={\rm E}_{r_{t},s_{t} \backsim E } [r(s_t,a_t)+\gamma Q^{\mu}(s_{t+1}, \mu (s_{t+1})) ] $$
- 위의 수식에 대한 추가설명
- 두 번째 수식에서 위의 수식으로 내려오면서 policy가 determinstic하기 때문에 policy에 dependent한 Expectation이 빠진 것을 알 수 있습니다.
- Deterministic policy를 가정하기 전의 수식에서는 $a_{t+1}$을 골랐던 순간의 policy로 Q에 대한 Expection을 원래 구해야하기 때문에 off-policy가 아니지만, Determinsitic policy를 가정한다면 update 할 당시의 policy로 $a_{t+1}$를 구할 수 있기 때문에 off-policy가 됩니다.
- Q learning
$$ L(\theta^{Q}) = {\rm E}_{s_t \backsim \rho^\beta , a_t \backsim \beta , r_t \backsim E} [(Q(s_t, a_t \vert \theta^Q)-y_t)^2] $$ - 위의 수식에 대한 추가설명
- $\beta$는 behavior policy를 의미합니다.
- $y_t = r(s_t, a_t) + \gamma Q^{\mu}(s_{t+1},\mu(s_{t+1}))$
- $\mu(s) = argmax_{a}Q(s,a)$
- Q learning은 위와 같이 $argmax$라는 deterministic policy를 사용하기 때문에 off policy로 사용할 수 있습니다.
2.3 DPG
$$ \nabla_{\theta^\mu} J \approx {\rm E}{s_t \backsim \rho^\beta} [ \nabla{\theta^\mu} Q(s, a \vert \theta ^ Q) \vert_{s=s_t, a=\mu(s_t)}] = {\rm E}{s_t \backsim \rho^\beta} [ \nabla{a} Q(s, a \vert \theta ^ Q) \vert_{s=s_t, a=\mu(s_t)} \nabla_{\theta^\mu} \mu(s \vert Q^{\mu})\vert_{s=s_t}] $$
- 위의 수식은 피지여행 DPG 글 4-2.Q-learning을 이용한 off-policy actor-critic에서 이미 정리 한 바 있습니다. DPG를 참고해주세요.
3. Algorithm
Continous control을 위한 새로운 알고리즘을 제안합니다. 제안하는 알고리즘의 특징은 다음과 같습니다.
- Replay buffer를 사용합니다.
- "soft" target update를 사용합니다.
- 각 차원의 scale이 다른 low dimension vector로 부터 학습할 때 Batch Normalization을 사용합니다.
- 탐험을 위해 action에 Noise를 추가합니다.
3.1 Replay buffer

- 큰 State space를 학습하고 일반화 하기위해서는 Neural Network와 같은 non-linear approximator가 필수적이지만 수렴한다는 보장이 없습니다.
- NFQCA에서는 수렴의 안정성을 위해서 batch learning을 도입합니다. 하지만 NFQCA에서는 업데이트시에 policy를 reset하지 않습니다.
- DDPG는 DQN에서 사용된 Replay buffer를 사용하여 online batch update를 가능하게 합니다.
3.2 Soft target update
$$ \theta^{Q^{'}} \leftarrow \tau \theta^{Q} + (1-\tau) \theta^{Q^{'}} $$
$$ \theta^{\mu^{'}} \leftarrow \tau \theta^{\mu} + (1-\tau) \theta^{\mu^{'}} $$
- DQN에서는 일정 주기마다 origin network의 weight를 target network로 직접 복사해서 사용합니다.
- DDPG에서는 exponential moving average(지수이동평균) 식으로 대체합니다.
- soft update가 DQN에서 사용했던 방식에 비해 어떤 장점이 있는지는 명확하게 설명되어있지 않지만 stochatic gradient descent와 같이 급격하게 학습이 진행되는 것을 막기 위해 사용하는 것 같습니다.
3.3 Batch Normalization

- 서로 scale이 다른 feature를 state로 사용할 때에 Neural Net이 일반화에서 어려움을 겪습니다.
- 이걸 해결하기 위해서는 원래 직접 스케일을 조정해주었습니다.
- 하지만 각 layer의 Input을 Unit Gaussian이 되도록 강제하는 BatchNormalization을 사용하여 이 문제를 해결합니다.
3.4 Noise Process
DDPG 에서는 Exploration을 위해서 output으로 나온 행동에 노이즈를 추가해줍니다.
ORNSTEIN UHLENBECK PROCESS(OU)
$$ dx_t = \theta (\mu - x_t) dt + \sigma dW_t $$
- OU Process는 평균으로 회귀하는 random process입니다.
- $\theta$는 얼마나 빨리 평균으로 회귀할 지를 나타내는 파라미터이며 $\mu$는 평균을 의미합니다.
- $\sigma$는 process의 변동성을 의미하며 $W_t$는 Wiener process를 의미합니다.
- 따라서 이전의 noise들과 temporally correlated입니다.
- 위와 같은 temporally correlated noise process를 사용하는 이유는 physical control과 같은 관성이 있는 환경에서 학습 시킬 때 보다 효과적이기 때문입니다.
3.5 Diagram & Pseudocode
- DDPG의 학습 과정을 간단히 도식화 해본 다이어그램입니다.

- DDPG의 알고리즘 수도코드입니다. 모든 항목을 위에서 설명했으니 순서대로 보시면 이해에 도움이 될것입니다.

4. Results
4.1 Variants of DPG
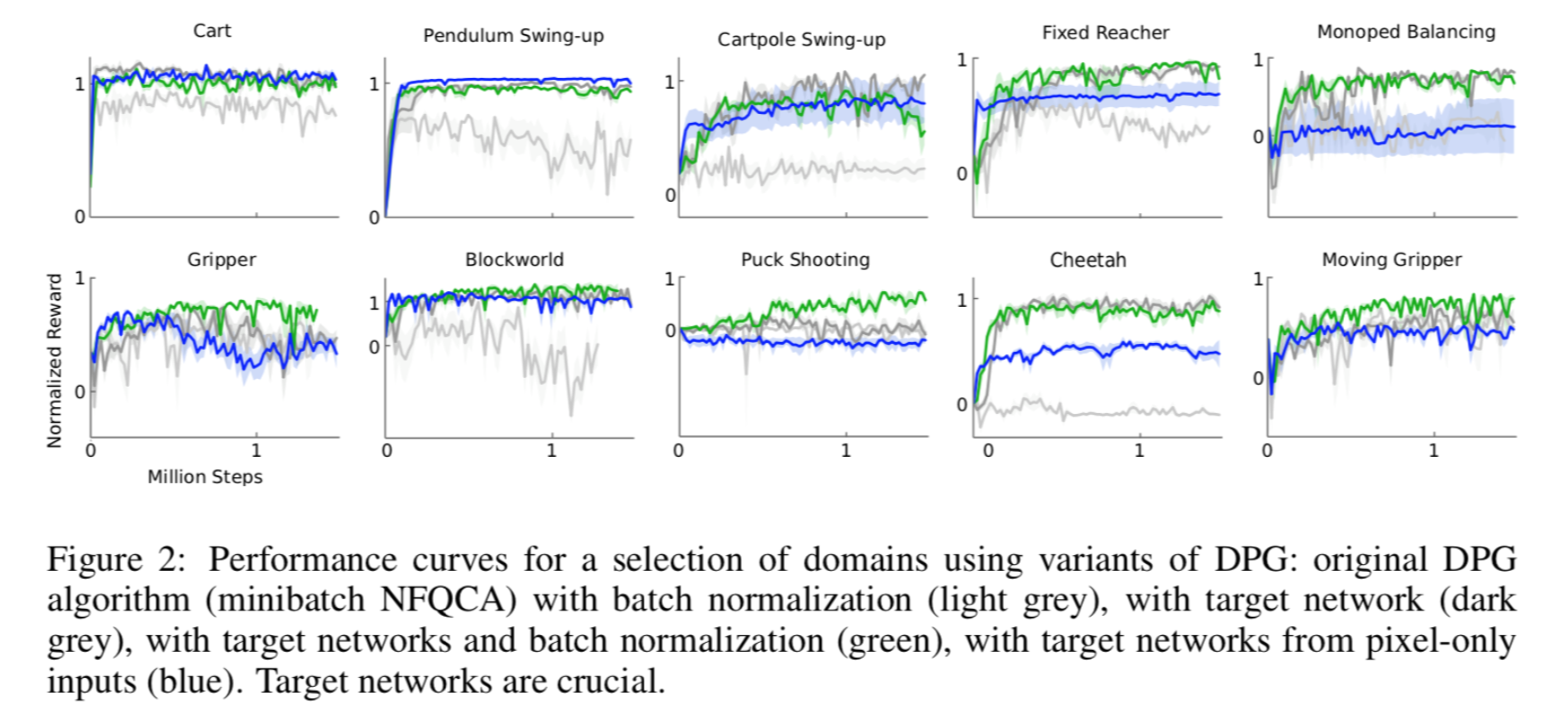
- original DPG에 batchnorm만 추가(연한 회색), target network만 추가(진한 회색), 둘 다 추가(초록), pixel로만 학습(파랑). Target network가 성능을 가장 좌지우지합니다.
4.2 Q estimation of DDPG

- DQN은 Q value를 Over-estimate하는 경향이 있었지만, DDPG는 simple task에 대해서는 잘한다. 복잡한 문제에 대해서는 estimation을 잘 못했지만, 여전히 좋은 Policy를 찾았습니다.
4.3 Performance Comparison

- Score는 naive policy를 0, ILQG (planning algorithm)의 mean score를 1점으로 놓았을 때의 점수 Torcs 환경에 대해서만 raw reward를 score로 사용합니다.
5. Implementation Details
5.1 Hyperparameters
- Optimizer: Adam
- actor LR: 0.0001, critic LR: 0.001
- Weight decay(L2) for critic(Q) : 0.001
- Discount factor : $\gamma = 0.99$
- Soft target updates : $\tau = 0.001$
- Size of replay buffer: 1,000,000
- Orstein Uhlenbeck Process : $\theta = 0.15$, $\sigma = 0.2$
5.2 Etc.
- Final output layer of actor : tanh (행동의 최소 최대를 맞춰주기 위해서)
- low-dimentional 문제에서 네트워크는 2개의 hidden layer (1st layer 400 units, 2nd layer 300 units)를 가집니다.
- 이미지를 통해서 학습시킬 때 : 3 convolutional layers (no pooling) with 32 filters at each layer.
- actor와 critic 각각의 final layer(weight, bias 모두)는 다음 범위의 uniform distribution에서 샘플링합니다. [ - 0.003, 0.003], [ - 0.0003 , 0.0003]. 이렇게 하는 이유는 가장 처음의 policy와 value의 output이 0에 가깝게 나오도록 하기 위합니다.
6. Conclusion
- 이 연구는 최근 딥러닝의 발전과 강화학습을 엮은 것으로 Continuous action space를 가지는 문제를 robust하게 풀어냅니다.
- non-linear function approximators을 쓰는 것은 수렴을 보장하지 않지만, 여러 환경에 대해서 특별한 조작 없이 안정적으로 수렴하는 것을 실험으로 보여냅니다.
- Atari 도메인에서 DQN보다 상당히 적은 step만에 수렴하는 것을 실험을 통해서 알아냅니다.
- model-free 알고리즘은 좋은 solution을 찾기 위해서는 많은 sample을 필요로 한다는 한계가 있지만 더 큰 시스템에서는 이러한 한계를 물리칠 정도로 중요한 역할을 하게 될 것이라고 합니다.
'프로젝트 > 피지여행' 카테고리의 다른 글
| 6. Trust Region Policy Optimization (0) | 2023.03.08 |
|---|---|
| 5. Natural Policy Gradient (0) | 2023.03.06 |
| 3. Deterministic Policy Gradient Algorithms (0) | 2023.03.05 |
| 2. Policy Gradient Methods for Reinforcement Learning with Function Approximation (0) | 2023.03.05 |
| 1. PG Travel Guide (0) | 2023.02.21 |
