피지여행 5번째 논문

논문 저자 : John Schulman, Sergey Levine, Philipp Moritz, Michael Jordan, Pieter Abbeel
논문 링크 : https://arxiv.org/pdf/1502.05477.pdf
Proceeding : International Conference on Machine Learning (ICML) 2015
정리 : 공민서, 김동민
1. 들어가며...
Trust region policy optimization (TRPO)는 상당히 우수한 성능을 보여주는 policy gradient 기법으로 알려져 있습니다. 높은 차원의 action space를 가진 robot locomotion부터 action은 적지만 화면을 그대로 처리하여 플레이하기 때문에 control parameter가 매우 많은 Atari game까지 각 application에 세부적으로 hyperparameter들을 특화시키지 않아도 두루두루 좋은 성능을 나타내기 때문에 일반화성능이 매우 좋은 기법입니다. 이 TRPO에 대해서 알아보겠습니다.
※TRPO를 매우 재밌게 설명한 Crazymuse AI의 Youtube video에서 일부 그림을 차용했습니다. 이 비디오를 시청하시는 것을 강력하게 추천합니다!
1.1 TRPO 흐름 잡기
TRPO 논문은 많은 수식이 등장하여 이 수식들을 따라가다보면 큰 그림을 놓칠 수도 있습니다. 세부적인 내용을 살펴보기 전에 기존 연구에서 출발해서 TRPO로 어떻게 발전해나가는지 간략하게 살펴보겠습니다.
1.1.1 Original Problem
$$ \max_\pi \eta(\pi) $$
모든 강화학습이 그렇듯이 expected discounted reward를 최대화하는 policy를 찾는 문제로부터 출발합니다.
1.1.2 Conservative policy iteration
$$ \max L_\pi(\tilde\pi) = \eta(\pi) + \sum_s \rho\pi(s)\sum_a\tilde\pi(a\vert s)A_\pi(s,a) $$
$\eta(\pi)$를 바로 최대화하는 것은 많은 경우 어렵습니다. $\eta(\pi)$의 성능향상을 보장하면서 policy를 update하는 conservative policy iteration 기법이 Kakade와 Langford에 의하여 제안되었습니다. 이 기법을 이용하면 policy update가 성능을 향상시키는지는 못하더라도 최소한 성능을 악화시키지는 않는다는 것이 이론적으로 보장됩니다.
1.1.3 Theorem 1 of TRPO
$$ \max L_{\pi_\mathrm{old} }\left(\pi_\mathrm{new}\right) - \frac{4\epsilon\gamma}{(1-\gamma)^2}\alpha^2,\quad\left(\alpha=D_\mathrm{TV}^{\max}\left(\pi_\mathrm{old},\pi_\mathrm{new}\right)\right) $$
기존의 conservative policy iteration은 과거 policy와 새로운 policy를 섞어서 사용해서 실용적이지 않다는 단점이 있었는데 이것을 보완하여 온전히 새로운 policy만으로 update할 수 있는 기법을 제안합니다.
1.1.4 KL divergence version of Theorem 1
$$ \max L_{\pi}\left(\tilde\pi\right) - C\cdot D_\mathrm{KL}^\max\left(\pi,\tilde\pi\right),\quad\left(C = \frac{4\epsilon\gamma}{(1-\gamma)^2}\right) $$
distance metric을 KL divergence로 바꿀 수 있습니다.
1.1.5 Using parameterized policy
$$ \max_\theta L_{\theta_\mathrm{old} }(\theta) - C\cdot D_\mathrm{KL}^\max\left(\theta_\mathrm{old}, \theta\right) $$
최적화문제를 더욱 편리하게 풀 수 있도록 낮은 dimension을 가지는 parameter들로 parameterized된 policy를 사용할 수 있습니다.
1.1.6 Trust region constraint
$$ \begin{align*} \max_\theta\quad &L_{\theta_\mathrm{old} }(\theta) \\ \mathrm{s.t.\ }&D_\mathrm{KL}^\max\left(\theta_\mathrm{old}, \theta\right) \leq \delta \end{align*} $$
1.1.5까지는 아직 conservative policy iteration을 약간 변형시킨 것입니다. policy를 update할 때 지나치게 많이 변하는 것을 방지하기 위하여 trust region을 constraint로 설정할 수 있습니다. 이 아이디어로 인해서 TRPO라는 명칭을 가지게 됩니다.
1.1.7 Heuristic approximation
$$ \begin{align*} \max_\theta\quad &L_{\theta_\mathrm{old} }(\theta) \\ \mathrm{s.t.\ }&\overline{D}_\mathrm{KL}^{\rho_\mathrm{old} }\left(\theta_\mathrm{old}, \theta\right) \leq \delta \end{align*} $$
사실 1.1.6의 constraint는 모든 state에 대해서 성립해야 하기 때문에 문제를 매우 어렵게 만듭니다. 이것을 좀 더 다루기 쉽게 state distribution에 대한 평균을 취한 것으로 변형합니다.
1.1.8 Monte Carlo simulation
$$ \begin{align*} \max_\theta\quad &E_{s\sim\rho_{\theta_\mathrm{old} },a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}Q_{\theta_\mathrm{old} }(s,a)\right] \\ \mathrm{s.t.\ }&E_{s\sim\rho_{\theta_\mathrm{old} }}\left[D_\mathrm{KL}\left(\pi_{\theta_\mathrm{old} }(\cdot\vert s) \parallel \pi_\theta(\cdot\vert s)\right)\right] \leq \delta \end{align*} $$
Sampling을 통한 계산이 가능하도록 식을 다시 표현할 수 있습니다.
1.1.9 Efficiently solving TRPO
$$ \begin{align*} \max_\theta\quad &\nabla_\theta \left. L_{\theta_\mathrm{old} }(\theta)\right\vert _{\theta=\theta_\mathrm{old} } \left(\theta - \theta_\mathrm{old}\right) \\ \mathrm{s.t.\ }&\frac{1}{2}\left(\theta_\mathrm{old} - \theta \right)^T A\left(\theta_\mathrm{old}\right)\left(\theta_\mathrm{old} - \theta \right) \leq \delta \\ &A_{ij} = \frac{\partial}{\partial \theta_i}\frac{\partial}{\partial \theta_j}\overline{D}_\mathrm{KL}^{\rho_\mathrm{old} }\left(\theta_\mathrm{old}, \theta\right) \end{align*} $$
문제를 효율적으로 풀기 위하여 approximation을 적용할 수 있습니다. objective function은 first order approximation, constraint는 quadratic approximation을 취하면 효율적으로 문제를 풀 수 있는 형태로 바뀌는데 이것을 natural gradient로 풀 수도 있고 conjugate gradient로 풀 수도 있습니다.
TRPO는 이렇게 다양한 방법으로 문제를 변형한 것입니다! 이제 좀 더 자세히 살펴보겠습니다.
2. Preliminaries
다음과 같은 파라미터를 가지는 infinite-horizon discounted Markov decision process (MDP)를 고려합니다.
- $\mathcal{S}$: finite set of states
- $\mathcal{A}$: finite set of actions
- $P: \mathcal{S}\times\mathcal{A}\rightarrow\mathbb{R}$: transition probability distribution
- $r: \mathcal{S}\rightarrow\mathbb{R}$: reward function
- $\rho_0:\mathcal{S}\rightarrow\mathbb{R}$: distribution of the initial state $s_0$
- $\gamma\in(0,1)$: discount factor
- $\eta(\pi)=E_{s_0,a_0,\ldots}\left[\sum_{t=0}^\infty\gamma^t r\left(s_t\right)\right]$, where $s_0\sim\rho_0\left(s_0\right), a_t\sim\pi\left(\left.a_t \right\vert s_t\right), s_{t+1}\sim P\left(\left.s_{t+1}\right\vert s_t,a_t\right)$
- $Q_\pi\left(s_t,a_t\right)=E_{ { \color{red}{s_{t+1}} },a_{t+1},\ldots}\left[\sum_{l=0}^\infty \gamma^l r\left(s_{t+l}\right)\right]$: action value function
- $V_\pi\left(s_t\right)=E_{ { \color{red}{a_t} }, s_{t+1},a_{t+1},\ldots}\left[\sum_{l=0}^\infty \gamma^l r\left(s_{t+l}\right)\right]$: value function (action value function과 expectation의 첨자가 다른 부분을 유의하세요.)
- $A_\pi(s,a) = Q_\pi(s,a) - V_\pi(s)$: advantage function
2.1 Useful identity [Kakade & Langford 2002]
우리의 목표는 $\eta(\pi)$가 최대화되도록 만드는 것입니다. 하지만 $\pi$의 변화에 따라 $\eta$가 어떻게 변하는지 알아내는 것도 쉽지 않습니다. $\pi$는 기존의 policy이고 $\tilde\pi$는 새로운 policy를 나타낸다고 할 때 $\eta$와 policy update 사이에 다음과 같은 관계가 있다는 것이 밝혀졌습니다.
Lemma 1. $\eta\left(\tilde\pi\right) = \eta(\pi) + E_{s_{0},a_{0},\ldots\sim\tilde\pi}\left[\sum_{t=0}^\infty\gamma^t A_\pi\left(s_t,a_t\right)\right]$
Proof. $A_\pi(s,a)=E_{s'\sim P\left(s'\vert s,a\right)}\left[r(s)+\gamma V_\pi\left(s'\right)-V_\pi(s)\right]$로 다시 표현할 수 있습니다. 표기의 편의를 위하여 $\tau:=\left(s_0,a_0,s_1,a_1,\ldots\right)$를 정의하겠습니다. 다음과 같은 수식 전개가 가능합니다.
$$ \begin{align*} &E_{\tau\vert \tilde\pi}\left[\sum_{t=0}^\infty\gamma^t A_\pi\left(s_t,a_t\right)\right] \\ &= E_{\tau\vert \tilde\pi}\left[\sum_{t=0}^\infty\gamma^t \left(r(s_t)+\gamma V_\pi\left(s_{t+1}\right)-V_\pi(s_t)\right)\right] \\ &= E_{\tau\vert \tilde\pi}\left[\left(\sum_{t=0}^\infty\gamma^t r(s_t)\right)+\gamma V_\pi\left(s_{1}\right)-V_\pi(s_0)+\gamma^2 V_\pi\left(s_{2}\right)-\gamma V_\pi(s_1)+\gamma^3 V_\pi\left(s_{3}\right)-\gamma^2 V_\pi(s_2)+\cdots\right] \\ &= E_{\tau\vert \tilde\pi}\left[\sum_{t=0}^\infty\gamma^t r(s_t)+\color{red}{\gamma V_\pi\left(s_{1}\right)}-V_\pi(s_0)+\color{red}{\gamma^2 V_\pi\left(s_{2}\right)}-\color{red}{\gamma V_\pi(s_1)}+\cdots\right] \\ &= E_{\tau\vert \tilde\pi}\left[-V_\pi(s_0)+\sum_{t=0}^\infty\gamma^t r(s_t)\right] \\ &\overset{\underset{\mathrm{(a)} }{} }{=} -E_{\color{red}{s_0}}\left[V_\pi(s_0)\right]+E_{\tau\vert \tilde\pi}\left[\sum_{t=0}^\infty\gamma^t r(s_t)\right] \\ &=-\eta(\pi) + \eta\left(\tilde\pi\right)\\ &\quad\therefore \eta\left(\tilde\pi\right) = \eta(\pi) + E_{s_{0},a_{0},\ldots\sim\tilde\pi}\left[\sum_{t=0}^\infty\gamma^t A_\pi\left(s_t,a_t\right)\right] \end{align*} $$
위의 전개의 (a) 부분은 $V_\pi\left(s_0\right)=E_{a_0,a_1,s_1,\ldots}\left[\sum_{t=0}^\infty\gamma^l r\left(s_l\right)\right]$이므로 $\tau$ 중 많은 부분들이 이미 expectation이 취해진 값이므로 무시됩니다. 오직 $s_0$만 expectation이 취해지지 않았기 때문에 남아있습니다.
Lemma 1은 새로운 policy와 기존의 policy 사이의 관계를 규정합니다. 다음과 같은 식을 정의하고 이것을 이용해서 Lemma 1을 변형시켜 봅시다.
- $\rho_\pi(s) = P\left(s_0=s\right) + \gamma P\left(s_1=s\right)\ + \gamma^2 P\left(s_2=s\right) + \cdots$ : (unnormalized) discounted visitation frequencies
$$ \begin{align*} \eta\left(\tilde\pi\right) &= \eta(\pi) + \sum_{t=0}^\infty\sum_{s}P\left(\left.s_t=s\right\vert \tilde\pi\right)\sum_a\tilde\pi(a\vert s)\gamma^t A_\pi(s,a) \\ &= \eta(\pi) + \sum_{s}{\color{red}{\sum_{t=0}^\infty \gamma^t P\left(\left.s_t=s\right\vert \tilde\pi\right)} } \sum_a\tilde\pi(a\vert s) A_\pi(s,a) \\ &= \eta(\pi) + \sum_{s}{\color{red}{\rho_\tilde\pi(s)} }\sum_a\tilde\pi(a\vert s) A_\pi(s,a) \\ \end{align*} $$
이 수식의 의미가 무엇일까요? 만약 $\sum_a\tilde\pi(a\vert s) A_\pi(s,a) \geq 0$이라면 $\eta(\tilde\pi)$는 항상 $\eta(\pi)$보다 큽니다. 즉, policy를 업데이트함으로써 항상 개선됩니다. 즉, 이 수식을 통해서 항상 더 좋은 성능을 내는 policy update가 가져야 할 특징을 알 수 있습니다. 다음과 같은 deterministic policy가 있다고 합시다.
$$ \tilde\pi(s) = \arg\max_a A_\pi(s,a) $$
이 policy는 적어도 하나의 state-action pair에서 0보다 큰 값을 가지는 advantage가 있고 그 때의 확률이 0이 아니라면 항상 성능을 개선시킵니다. 어려운 점은 policy를 바꾸면 $\rho$도 바뀐다는 점입니다.
다음 그림을 봅시다. Starting Point에서 여러가지 경로를 거쳐서 Destination으로 갈 수 있습니다. 다른 policy를 이용하는 것은 다른 경로를 이용한 것입니다.

이 때 다른 policy를 이용함에 따라 state visitation frequency도 변하게 됩니다.

이로 인해서 policy를 최적화하는 것은 어려워집니다. 그래서 이러한 변화를 무시하는 다음과 같은 approximation을 취합니다.
$$ \begin{align*} L_\pi\left(\tilde\pi\right) &= \eta(\pi) + \sum_{s}{\color{red}{\rho_\pi(s)} } \sum_a\tilde\pi(a\vert s) A_\pi(s,a) \end{align*} $$
policy가 바뀌었음에도 이전의 state distribution을 계속 이용하는 것입니다. 이것은 policy의 변화가 크지 않다면 어느 정도 허용될 수 있을 것입니다. 그렇지만 얼마나 많은 변화가 허용될까요? 이것을 정하기 위해서 이용하는 것이 trust region입니다.
2.2 Conservative Policy Iteration
policy의 변화를 다루기 용이하게 하기 위해서 policy를 다음과 같이 파라미터를 이용해서 표현합시다.
- $\pi_\theta(a\vert s)$: parameterized policy
$\pi_\theta$는 $\theta$에 대하여 미분가능한 함수입니다. $L_\pi\left(\tilde\pi\right)$을 $\theta_0$에서 $\eta(\pi)$에 대한 first order approximation이라고 하면 다음 식이 성립합니다.
$$ \begin{align*} L_{\pi_{\theta_0} }\left(\pi_{\theta_0}\right) &= \eta\left(\pi_{\theta_0}\right) \\ \nabla_\theta \left.L_{\pi_{\theta_0} }\left(\pi_{\theta_0}\right)\right\vert _{\theta=\theta_0} &= \nabla_\theta\left.\eta(\pi_{\theta_0})\right\vert _{\theta=\theta_0} \end{align*} $$
이것의 의미는 $\pi_{\theta_0}$가 매우 작게 변한다면 $L_{\pi_{\theta_0} }$를 개선시키는 것이 $\eta$를 개선시키는 것이라는 것입니다. 그러나 지금까지의 설명만으로는 $\pi_{\theta_0}$를 얼마나 작게 변화시켜야 할지에 대해서는 알 수 없습니다.
Kakade & Langford가 2002년 발표한 논문에서도 이것에 대해서 고민했습니다. 그 논문에서 conservative policy iteration이라는 기법을 제안합니다. 그 논문의 contribution은 다음과 같습니다.
- $\eta$ 개선의 lower bound를 제공
- 기존의 policy를 $\pi_\mathrm{old}$라고 하고 $\pi'$를 $\pi’=\arg\max_{\pi’}L_{\pi_\mathrm{old} }\left(\pi’\right)
$과 같이 정의할 때, 새로운 mixture policy $\pi_\mathrm{new}$를 다음과 같이 제안
$$ \pi_\mathrm{new}(a\vert s) = (1-\alpha)\pi_\mathrm{old}(a\vert s) + \alpha \pi'(a\vert s) $$
그림으로 표현하면 다음과 같습니다.

- 다음과 같은 lower bound를 정의
$$ \eta\left(\pi_\mathrm{new}\right) \geq L_{\pi_{\theta_\mathrm{old} }}\left(\pi_\mathrm{new}\right) - \frac{2\epsilon\gamma}{(1-\gamma)^2}\alpha^2,\\ \mathrm{where\ }\epsilon = \max_s\left\vert E_{a\sim\pi’(a\vert s)}\left[A_\pi(s,a)\right]\right\vert $$
하지만 mixture된 policy라는 것은 실용적이지 않습니다.
3. Monotonic Improvement Guarantee for General Stochastic Policies
이전 장에서 설명한 lower bound는 오직 mixture policy에 대해서만 성립하고 더 많이 사용되는 stochastic policy에는 적용되지 않습니다. 따라서 stochastic policy를 이용할 수 있도록 개선할 필요가 있습니다. 아래와 같이 기존 수식에서 두 가지를 바꿈으로써 이것이 가능합니다.
- $\alpha\rightarrow$ distance measure between $\pi$ and $\tilde\pi$
- constant $ \epsilon\rightarrow\max_{s,a}\left\vert A_\pi(s,a)\right\vert $
여기서 distance measure로 total variation divergence를 이용합니다. discrete porbability distribution $p$와 $q$에 대하여 다음과 같이 정의됩니다.
$$ D_\mathrm{TV}(p \parallel q) = \frac{1}{2}\sum_i\left\vert p_i - q_i\right\vert $$
이것을 이용하여 $D_\mathrm{TV}^\max$를 다음과 같이 정의합니다.
$$ D_\mathrm{TV}^\max(\pi\parallel \tilde\pi) = \max_s D_\mathrm{TV}\left(\pi(\cdot\vert s)\parallel\tilde\pi(\cdot\vert s)\right) $$
그림으로 표현하면 다음과 같습니다.

이것을 이용하여 다음과 같은 관계식을 얻을 수 있습니다.
Theorem 1. Let $ \alpha=D_\mathrm{TV}^\max(\pi\parallel \tilde\pi) $. Then the following bound holds:
$$ \begin{align*} \eta\left(\pi_\mathrm{new}\right) &\geq L_{\pi_\mathrm{old} }\left(\pi_\mathrm{new}\right) - \frac{4\epsilon\gamma}{(1-\gamma)^2}\alpha^2, \\ \mathrm{where\ } \epsilon&= \max_{s,a}\left\vert A_\pi(s,a)\right\vert \end{align*} $$
또다른 distance metric으로 아래 그림과 같은 KL divergence가 있습니다. (그런데 왜 하필 KL divergence로 바꿀까요? 논문의 뒤쪽에서 계산효율을 위해서 conjugate gradient method를 이용하는데 이를 위해서 바꾼게 아닐까 싶습니다. Wasserstein distance 같은 다른 방향으로 발전시킬 수도 있을 것 같습니다. Schulmann이 아마 해봤겠죠?^^a)

total variation divergence와 KL divergence 사이에는 다음과 같은 관계가 있습니다.
$$ D_\mathrm{TV}(p\parallel q)^2 \leq D_\mathrm{KL}(p\parallel q) $$
다음 수식을 정의합니다.
$$ D_\mathrm{KL}^\max(\pi\parallel \tilde\pi) = \max_s D_\mathrm{KL}\left(\pi(\cdot\vert s)\parallel\tilde\pi(\cdot\vert s)\right) $$
Theorem 1을 이용하여 다음과 같은 수식이 성립함을 알 수 있습니다.
$$ \begin{align*} \eta\left(\tilde\pi\right) &\geq L_{\pi}\left(\tilde\pi\right) - C\cdot D_\mathrm{KL}^\max(\pi, \tilde\pi), \\ \mathrm{where\ } C&= \frac{4\epsilon\gamma}{(1-\gamma)^2} \end{align*} $$
이러한 policy imporvement bound를 기반으로 다음과 같은 approximate policy iteration 알고리듬을 고안해낼 수 있습니다.
Algorithm 1 Policy iteration algorithm guaranteeing non-decreasing expected return $\eta$

Algorithm 1은 advantage를 정확하게 계산할 수 있다고 가정하고 있습니다. 이 알고리듬은 monotonical한 성능 증가($\eta(\pi\_0)\leq\eta(\pi\_1)\leq\cdots$)를 한다는 것을 다음과 같이 보일 수 있습니다. $M_i(\pi)=L_{\pi_i}(\pi) - CD_\mathrm{KL}^\max\left(\pi_i,\pi\right)$라고 합시다.
$$ \begin{align*} \eta \left(\pi_{i+1}\right) &\geq M_i\left(\pi_{i+1}\right)\\ \eta \left(\pi_{i}\right) &= M_i\left(\pi_{i}\right) \\ \eta \left(\pi_{i+1}\right) - \eta \left(\pi_{i}\right) &\geq M_i\left(\pi_{i+1}\right) - M_i\left(\pi_{i}\right) \end{align*} $$
위 수식과 같이 매 iteration 마다 $M\_i$를 최대화함으로써, $\eta$가 감소하지 않는다는 것을 보장할 수 있습니다. 이와 같은 타입의 알고리듬을 minorization-maximization (MM) algorithm이라고 합니다. EM 알고리듬도 이 타입의 알고리듬 중 하나입니다.
Algorithm 1은 아래 그림과 같이 동작합니다.

$M_i$는 $\pi_i$일 때 equality가 되는 $\eta$에 대한 surrogate function입니다. TRPO는 이 surrogate function을 최대화하고 KL divergence를 penalty가 아닌 constraint로 두는 알고리듬입니다.
4. Optimization of Parameterized Policies
표기의 편의를 위해 다음과 같이 notation들을 더 간략하게 정의합니다.
- $\eta(\theta):=\eta\left(\pi_\theta\right)$
- $L_\theta\left(\tilde\theta\right):=L_{\pi_\theta}\left(\pi_{\tilde\theta}\right)$
- $D_\mathrm{KL}\left(\theta\parallel\tilde\theta\right):=D_\mathrm{KL}\left(\pi_\theta\parallel\pi_{\tilde\theta}\right)$
- $\theta_\mathrm{old}$: previous policy parameter
4.1 Trust Region Policy Optimization
이전 장의 중요 결과를 위의 notation으로 다시 표기하면 아래와 같습니다.
$$ \eta\left(\theta\right) \geq L_{\theta_\mathrm{old} }\left(\theta\right) - C\cdot D_\mathrm{KL}^\max\left(\theta_\mathrm{old}, \theta\right) $$
$\eta$의 성능 향상을 보장하기 위해서 그것의 lower bound를 최대화할 수 있습니다.
$$ \max_\theta \left[L_{\theta_\mathrm{old} }\left(\theta\right) - C D_\mathrm{KL}^\max\left(\theta_\mathrm{old}, \theta\right)\right] $$
이 최적화 문제는 step size를 매우 작게 해야 올바른 동작을 합니다. 위에서 살펴봤듯이 first order approximation이기 때문입니다. 좀 더 큰 step size를 가질 수 있도록 이 최적화 문제를 trust region constraint를 도입하여 다음과 같이 바꿉니다.
$$ \begin{align*} \max_\theta\quad &L_{\theta_\mathrm{old} }(\theta) \\ \mathrm{s.t.\ }&D_\mathrm{KL}^\max\left(\theta_\mathrm{old}, \theta\right) \leq \delta \end{align*} $$
이 최적화문제의 constraint는 모든 state space에 대해서 성립해야 합니다. 또한 maximum값을 매번 찾아야 합니다. state가 많은 경우 constraint의 수가 매우 많아져서 문제를 풀기 어렵게 만듭니다. constraint의 수를 줄이기 위하여 다음과 같은 avergae KL divergence를 이용하는 heuristic approximation을 취합니다. 이것이 최선의 방법은 아닐 수 있지만 실용적인 방법입니다.
$$ \overline D_\mathrm{KL}^{\rho}\left(\theta_1, \theta_2\right):=E_{s\sim\rho}\left[D_\mathrm{KL}\left(\pi_{\theta_1}(\cdot\vert s)\parallel\pi_{\theta_2}(\cdot\vert s)\right)\right] $$
이것을 기반으로 다음과 같은 최적화 문제를 풀 수 있습니다.
$$ \begin{align} \max_\theta\quad &L_{\theta_\mathrm{old} }(\theta) \\ \mathrm{s.t.\ }&\overline{D}_\mathrm{KL}^{\rho_\mathrm{old} }\left(\theta_\mathrm{old}, \theta\right) \leq \delta \end{align} $$
아래 그림처럼 step size에 대해서 고려할 수 있습니다.

5. Sample-Based Estimation of the Objective and Constraint
실용적인 알고리듬을 만들려고 하는 노력은 아직 끝나지 않았습니다. 이제 앞의 알고리듬을 sample-based estimation 즉, Monte Carlo estimation을 할 수 있도록 바꿔보겠습니다. sampling을 편하게 할 수 있도록 아래와 같이 바꿔줍니다.
- $\sum_s \rho_{\theta_\mathrm{old} }(s)[\ldots]\rightarrow\frac{1}{1-\gamma}E_{s\sim\rho_{\theta_\mathrm{old} }}[\ldots] $
- $A_{\theta_\mathrm{old} }\rightarrow Q_{\theta_\mathrm{old} } $
- $\sum_a\pi_{\theta_\mathrm{old} }(a\vert s)A_{\theta_\mathrm{old} } \rightarrow E_{a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}A_{\theta_\mathrm{old} }\right] $
이러한 변화를 그림처럼 도식화할 수 있습니다.

한 가지 짚고 넘어가야 할 점은 action sampling을 할 때 importance sampling을 사용한다는 것입니다.

바뀐 최적화문제는 아래와 같습니다.
- Equation (14).
$$ \begin{align*} \max_\theta\quad &E_{s\sim\rho_{\theta_\mathrm{old} },a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}Q_{\theta_\mathrm{old} }(s,a)\right] \\ \mathrm{s.t.\ }&E_{s\sim\rho_{\theta_\mathrm{old} }}\left[D_\mathrm{KL}\left(\pi_{\theta_\mathrm{old} }(\cdot\vert s) \parallel \pi_\theta(\cdot\vert s)\right)\right] \leq \delta \end{align*} $$
이 때 sampling하는 두 가지 방법이 있습니다.
5.1 Single Path
single path는 개별 trajectory들을 이용하는 방법입니다.

5.2 Vine
vine은 한 state에서 rollout을 이용하여 여러 action을 수행하는 방법입니다.
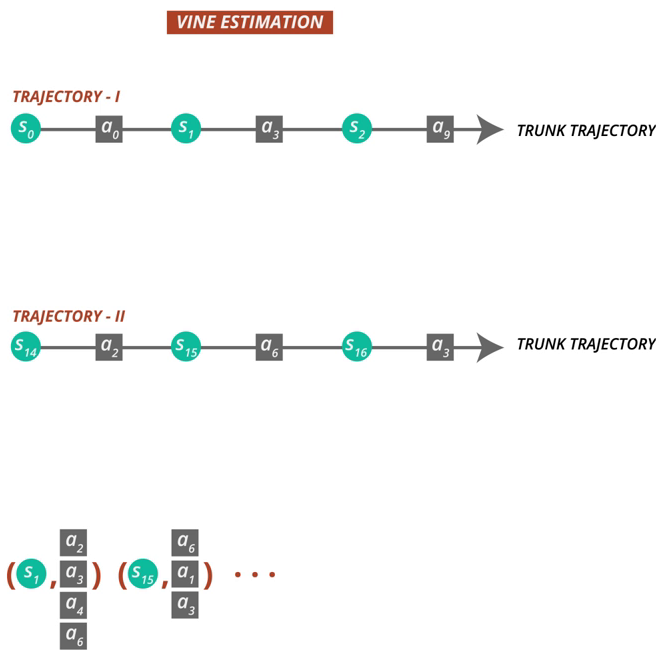

estimation의 variance를 낮출 수 있지만 계산량이 많고 한 state에서 여러 action을 수행할 수 있어야 하기 때문에 현실적인 문제에 적용하기에는 어려움이 있습니다.
6. Practical Algorithm
앞서 single-path, vine 샘플링을 사용하는 두가지 방식의 policy optimization 알고리즘을 살펴봤습니다. 실용적인 알고리듬은 아래의 과정을 반복해서 수행합니다.
- Q-values의 몬테카를로 추정을 통해 state-action 쌍 집합을 single path 또는 vine 과정을 통해 수집함.
- 샘플 평균으로, (14)식의 목적함수와 제약식을 추정함
Equation (14).
$$ \begin{align*} \max_\theta\quad &E_{s\sim\rho_{\theta_\mathrm{old} },a\sim q}\left[\frac{\pi_\theta(a\vert s)}{q(a\vert s)}Q_{\theta_\mathrm{old} }(s,a)\right] \\ \mathrm{s.t.\ }&E_{s\sim\rho_{\theta_\mathrm{old} }}\left[D_\mathrm{KL}\left(\pi_{\theta_\mathrm{old} }(\cdot\vert s) \parallel \pi_\theta(\cdot\vert s)\right)\right] \leq \delta \end{align*} $$ - policy parameter vector인 $\theta$를 업데이트 하면서 제약조건이 있는 최적화 문제를 근사적으로 풂. 본 논문에서는 gradient를 직접 계산하는 것보다는 약간 더 계산량이 있는 line search와 conjugate gradient algorithm을 사용했습니다.
3)에 대해서, gradient의 covariance matrix를 사용하지 않고 KL divergence의 Hessian을 해석적으로 계산하여 Fisher Information Matrix를 구성했습니다.
다시말해서
$\frac{1}{N} \sum_{n=1}^{N} \frac{\partial}{\partial \theta_i} \log \pi_{\theta}(a_n\vert s_n) \frac{\partial}{\partial \theta_j} \log \pi_{\theta}(a_n\vert s_n)$ 대신 $\frac{1}{N} \sum_{n=1}^{N} \frac{\partial^2}{\partial \theta_i \partial \theta_j} D_{KL}(\pi_{\theta_{old} }(\cdot \vert s_n) \vert \vert \pi_{\theta}(\cdot \vert s_n))$를 계산한 것입니다.
이 analytic estimator는 Hessian이나 trajectories의 모든 gradient를 저장하지 않아도 되기 때문에 대규모 환경을 고려할 경우 계산 상 이점이 있습니다. 좀 더 자세하게 설명한 Appendix C 부분을 살펴보겠습니다.
Appendix C. Efficiently Solving the Trust-Region Constrained Optimization Problem
우리가 풀고자 하는 식은 다음과 같습니다.
$$ \begin{align*} \max\quad &L(\theta) \\ \mathrm{s.t.\ } &\overline{D}_{KL}(\theta_\mathrm{old}, \theta) \leq \delta \end{align*} $$
이 최적화 문제를 풀기 위하여 우리는 gradient 기법을 이용할 것입니다. gradient 기법은 결국 update할 방향과 크기를 결정하는 문제로 생각할 수 있습니다. 이에 따라 아래와 같은 두가지 과정으로 진행합니다.
- 탐색 방향을 계산, 목적함수의 first-order approximation(선형근사)와 제약식의 quadratic approximation(2차 근사).
- 이동거리 계산을 위해 해당 방향으로 line search 수행.
탐색 방향은 $Ax = g$ 수식을 근사적으로 풀어서 구합니다. 여기서 $A$ 는 Fisher Information Matrix이고, 이것은 KL divergence 제약식의 2차 근사 $ \overline{D}_\mathrm{KL} (\theta_\mathrm{old}, \theta) \approx \frac{1}{2}(\theta - \theta_\mathrm{old})^T A(\theta - \theta_\mathrm{old}) $를 푸는 것입니다. 여기서 $ A_{ij} = \frac{\partial}{\partial \theta_i} \frac{\partial}{\partial \theta_j} \overline{D}_\mathrm{KL}(\theta_\mathrm{old}, \theta) $입니다.
논문에서 이 부분에 대한 설명이 약간 부족해서 좀 더 내용을 추가하자면, $\frac{1}{2}x^T A x - x^T g + b = 0$과 같은 quadratic equation의 해는 1차 derivative를 0으로 만드는 $x$를 찾음으로써 알 수 있습니다. 위에서 우리는 목적함수를 1차 근사시키고 제약조건은 2차 근사를 시킴으로써 quadratic equation 형태로 변형했기 때문에 같은 방식으로 풀 수 있습니다. 따라서 $g$는 1차근사시킨 목적함수의 계수가 될 것입니다.
대규모 문제에서 $A$ 혹은 $A^{-1}$ 을 계산하는 것은 엄청난 계산량이 필요합니다. 하지만 conjugate gradient algorithm을 잘 이용하면 전체 $A$행렬(FIM)을 계산하지 않아도 $Ax=g$ 를 근사적으로 해결할 수 있게 해줍니다.
탐색 방향 $s \approx A^{-1}g$과 더불어 최대스텝길이(step size) $\beta$도 계산할 필요가 있습니다.
즉, $ \delta = \overline{D}_\mathrm{KL} \approx \frac{1}{2}(\beta s)^T A(\beta s) = \frac{1}{2}\beta^2s^TAs $ 이고,
$\beta = \sqrt{2\delta / s^T As}$가 됩니다. 이때 $\delta$는 KL divergence의 boundary term 입니다.
$s^T As$ 항은 Hessian-vector product로 계산할 수 있고, conjugate gradient 과정에서 계산됩니다.
마지막으로, surrogate objective와 KL divergence 제약식을 위해 다음과 같은 함수를 정의하고 line search를 사용합니다.
$$ L_{\theta_\mathrm{old} }(\theta) - \chi [\overline{D}_{KL}(\theta_\mathrm{old}, \theta) \leq \delta] $$
$\chi[\cdot]$ 함수는 []안의 조건이 맞으면 0이고 틀리면 무한으로 발산하는 함수입니다.
위에서 계산한 $\beta$ 의 최대 값부터 시작해서 목적함수가 개선될때까지 exponential하게 줄여 나갑니다. line search가 없었다면 이 알고리즘은 매우 큰 스텝으로 계산될 것이고 심각한 성능 저하가 발생할 것입니다.
(여기서 살짝 예고를 하자면, 나중에 이 KL 기반 기법을 개선한 더 단순한 방법이 제안됩니다. PPO라고...)
7. Connections with Prior Work
Natural Policy Gradient는 $L$의 선형 근사와 $\overline D_\mathrm{KL}$ 제약식을 2차근사 하는 아래의 식의 special case입니다.
- Equation (17).
$L_{\pi}(\tilde\pi) = \eta(\pi) + \underset{s}{\sum}\rho_{\pi}(s) \underset{a}{\sum}\tilde\pi(a\vert s)A_\pi(s,a) $
$\underset{\theta}{\max}\quad [\nabla_{\theta}L_{\theta_\mathrm{old} }(\theta) \ \rvert_{\theta=\theta_\mathrm{old} } \cdot (\theta - \theta_\mathrm{old})] $
$ \mathrm{s.t.}\quad\frac{1}{2}(\theta_\mathrm{old} - \theta)^{T} A(\theta_\mathrm{old})(\theta_\mathrm{old}-\theta) \leq \delta $
$ \mathrm{where\ }A(\theta_{old})_{ij} = $
$\Large \frac{\partial}{\partial \theta_{i} } \frac{\partial}{\partial \theta_{j} } E_{s \sim \rho_{\pi} }[D_\mathrm{KL}(\pi(\cdot\rvert s, \theta_\mathrm{old}) \rvert\rvert \pi(\cdot \rvert s, \theta))] \rvert_{\theta=\theta_\mathrm{old} } $
업데이트 식은 다음과 같습니다.
$\theta_\mathrm{new} = \theta_\mathrm{old} + \color{Red}{\frac{1}{\lambda} } A(\theta_\mathrm{old})^{-1}\nabla_{\theta}L(\theta) \rvert_{\theta=\theta_\mathrm{old} } $
여기서 step size인 $\frac{1}{\lambda}$ 일반적으로 알고리즘의 파라미터로 취급되지만 TRPO는 각 업데이트 마다 제약식으로 사용한다는 점이 다릅니다. 사소한 차이처럼 보이지만, 큰 차원을 다루는 실험에서 성능을 크게 향상시켰습니다.
또한 $L^2$ 제약식(혹은 페널티) 를 사용하면 표준 Policy Gradient 업데이트 식을 얻었습니다.
- Equation (18).
$\underset{\theta}{\max}\quad[\nabla_{\theta} L_{\theta_\mathrm{old} }(\theta) \rvert_{\theta=\theta_\mathrm{old} } \cdot (\theta - \theta_\mathrm{old})] $
$ \mathrm{s.t.}\quad \frac{1}{2} \vert\vert \theta - \theta_\mathrm{old} \vert\vert^2 \leq \delta $
$L_{\pi}(\tilde\pi) = \eta(\pi) + \underset{s}{\sum}\rho_{\pi}(s) \underset{a}{\sum}\tilde\pi(a\vert s)A_\pi(s,a) $를 이용해서 제약조건없이 $\underset{\pi}{\max}\quad L_{\pi_\mathrm{old} }(\pi) $를 풀면 Policy Iteration update를 하는 것과 같습니다.
8. Experiments
- 다음과 같은 3 가지 궁금증을 해결하기 위하여 실험을 설계하였습니다.
- Single-path 와 vine 의 성능면에서 특징을 알고싶음.
- Fixed penalty coefficient(NPG) 보다 fixed KL divergence를 사용하는 것(TRPO)으로 변경한 것이 얼마나 뚜렷한 차이를 보일지, 성능 면에서 어떤 영향을 미치는지 알고싶음.
- TRPO가 큰 스케일의 문제를 해결할 수 있는지, 기존에 연구/적용되어왔던 방법들과 성능, 계산시간, 샘플 복잡도 면에서 비교하고 싶음.
- 1, 2의 궁금증에 대해서 실험 환경에 single path, vine을 비롯한 여러 사전방법들을 함께 실험하였습니다.
- 3에 대해선, robotic locomotion과 Atari game에 TRPO를 실험하였습니다.
8.1 Simulated Robotic Locomotion
- MuJoCo 시뮬레이터를 활용해 로봇 locomotion 실험 진행하였습니다.
- Robot State: positions and velocities, joint torques

- 수영, 점프, 걷기 행동을 학습시키고자 합니다.
- 수영: 10 dimensional state space , reward: $r(x,u)=v_x - 10^{-5}\vert \vert u\vert \vert ^2$, quadratic penalty.
- 점프: 12 dimensional state space, episode의 끝은 높이와 각도 threshol로 점프를 판단, non-terminal state에 대해 +1 보상 추가.
- 걷기: 18 dimensional state space, 뜀뛰는 듯한 보법(점프에이전트)보다 부드러운 보법을 유도하기위해 페널티를 추가함.
Detailed Experiment Setup and used parameters, used network model


equation (12) : $ \max\quad L_{\theta_\mathrm{old}(\theta)}, \ \ \mathrm{s.t.\ }\overline{D}_\mathrm{KL}^{\rho_{\theta_\mathrm{old} }}(\theta_\mathrm{old}, \theta) \leq \delta $
이 실험에서 $\delta = 0.01$입니다.
- 비교에 사용된 모델들
- TRPO Single-path
- TRPO vine
- CEM(cross-entropy method)
- CMA(covariance matrix adaptation)
- NPG (Lagrange Multiplier penalty coefficien를 사용하는 것이 차이점)
- Empirical FIM
- maximum KL(cartpole)

- 제안한 single path, vine 모두 task를 잘 학습하는 것을 확인할 수 있습니다.
- 페널티를 고정하는 것보다, KL divergenc를 제약하는 것이 step size를 선택하는 부분에서 Robust합니다.
- CEM/CMA는 derivative free 알고리즘으로, 샘플 복잡도가 네트워크 파라미터수 만큼 확장되어 high dimension 문제에서는 속도와 성능이 약한 모습을 보입니다.
- maxKL은 제안방법보다 느린 학습성능을 보입니다.
TRPO video link: https://www.youtube.com/watch?v=jeid0wIrSn4
- YouTube
www.youtube.com
- 사전지식이 적은 상태에서 여러 액션을 학습하는 실험으로 TRPO의 성능을 보입니다.
- 지금까지의 균형이나 걸음 같은 개념을 명시적으로 인코딩한 robotic locomotion에서의 사전 연구들과 차이를 보였습니다.
8.2 Playing Games from Images
- 부분관찰가능하며 복잡한 observation인 환경에서 TRPO를 평가하기위해 raw image를 입력으로 하는 아타리게임 환경에서 실험하였습니다.
- Challenging point :
- High dimensional space
- delayed reward
- non-stationary image (Enduro는 배경 이미지가 바뀌고, 반전처리가 됨)
- complex action sequence (Q*bert는 21개의 다른 발판에서 점프 해야함)
- ALE(Arcade Learning Environment) 에서 테스트
- DQN과 전처리 방식은 동일 210 x 160 pixel → gray-scaling & down-sampling → 110 x 84 → crop → 84 x 84
- 2 convolution layer ( 16 channels) , stride 2, FC layer with 20 units



- 30시간 동안 500 iteration 학습을 하였습니다.
- DQN과 MCST를 사용한 모델(UCC-I), 사람이 플레이한 것(Human) 과의 비교하였습니다.
- 이전 방법들에 비해 압도적인 점수를 기록하진 못했으나, 다양한 게임에서 적절한 게임 기록하였습니다.
- 이전 방법들과 다른 점은, 특정 task에 초점을 맞춰 설계하지않았는데 robotics나 game playing Task에도 적절한 성능을 내는 점에서 TRPO의 일반화 성능을 확인하였습니다.
9. Discussion
- Trust Region Policy Optimization 을 제안하였습니다.
- KL Divergence 페널티로 $\eta(\pi)$를 최적화하는 알고리즘이 monotonically improve 함을 증명하였습니다.
- Locomotion 도메인에서 여러 행동(수영, 걷기, 점프)을 제어하는 controller를 학습하였습니다.
- Robotics와 게임 실험을 결합해, 시각정보와 센서데이터를 사용하는 로봇제어 정책을 학습시킬 수 있는 가능성을 보았습니다.
- 샘플의 복잡도를 상당히 줄일 수 있어 실제상황에 적용가능성을 보았습니다.
GitHub - reinforcement-learning-kr/pg_travel: Policy Gradient algorithms (REINFORCE, NPG, TRPO, PPO)
Policy Gradient algorithms (REINFORCE, NPG, TRPO, PPO) - GitHub - reinforcement-learning-kr/pg_travel: Policy Gradient algorithms (REINFORCE, NPG, TRPO, PPO)
github.com
'프로젝트 > 피지여행' 카테고리의 다른 글
| 8. Proximal Policy Optimization (0) | 2023.03.12 |
|---|---|
| 7. High-Dimensional Continuous Control using Generalized Advantage Estimation (0) | 2023.03.12 |
| 5. Natural Policy Gradient (0) | 2023.03.06 |
| 4. Deep Deterministic Policy Gradient (DDPG) (0) | 2023.03.06 |
| 3. Deterministic Policy Gradient Algorithms (0) | 2023.03.05 |
