피지여행 2번째 논문

논문 저자 : David Silver, Guy Lever, Nicloas Heess, Thomas Degris, Daan Wierstra, Martin Riedmiller
논문 링크 : main text, supplementary material
Proceeding : International Conference on Machine Learning (ICML)
2014 정리 : 김동민, 공민서, 장수영, 차금강
1. 들어가며...
- Deterministic Policy Gradient (DPG) Theorem을 제안합니다.
- 중요한 점은 DPG는 Expected gradient of the action-value function의 형태라는 것입니다.
- Policy variance가 0에 수렴할 경우, DPG는 Stochastic Policy Gradient (SPG)와 동일해집니다. (Theorem 2)
- Theorem 2로 인해 기존 Policy Gradient (PG) 와 관련된 기법들을 DPG에 적용할 수 있게 됩니다.
- 예. Sutton PG, natural gradients, actor-critic, episodic/batch methods
- Theorem 2로 인해 기존 Policy Gradient (PG) 와 관련된 기법들을 DPG에 적용할 수 있게 됩니다.
- 적절한 exploration 을 위해 model-free, off-policy actor-critic algorithm 을 제안합니다
- action-value function approximator 사용으로 인해 policy gradient가 bias되는 것을 방지하기 위해 compatibility condition을 제공합니다. (Theorem 3)
- DPG 는 SPG 보다 성능이 좋습니다.
- 특히 high dimensional action spaces를 가지는 tasks에서의 성능 향상이 큽니다.
- SPG의 policy gradient는 state와 action spaces 모두에 대해서, DPG의 policy gradient는 state spaces에 대해서만 평균을 취합니다.
- 결과적으로, action spaces의 dimension이 커질수록 data efficiency가 높은 DPG의 학습이 더 잘 이뤄지게 됩니다.
- 무한정 학습을 시키면, SPG도 최적으로 수렴할 것으로 예상되기에 위 성능 비교는 일정 iteration 내로 한정합니다.
- 기존 기법들에 비해 computation 양이 많지 않습니다.
- Computation 은 action dimensionality 와 policy parameters 수에 비례합니다.
- 특히 high dimensional action spaces를 가지는 tasks에서의 성능 향상이 큽니다.
2. Background
2.1 Performance objective function
$$ \begin{align} J(\pi_{\theta}) &= \int_{S}\rho^{\pi}(s)\int_{A}\pi_{\theta}(s,a)r(s,a)da ds = E_{s \sim \rho^{\pi}, a \sim \pi_{\theta}}[r(s,a)] \end{align} $$
2.2 SPG Theorem
- State distribution $\rho^{\pi}(s)$ 은 policy parameters에 영향을 받지만, policy gradient 를 계산할 때는 state distribution 의 gradient 를 고려할 필요가 없습니다.
$$ \nabla_{\theta}J(\pi_{\theta}) = \int_{S}\rho^{\pi}(s)\int_{A}\nabla_{\theta}\pi_{\theta}(a|s)Q^{\pi}(s,a)dads \\ \ \\ = E_{s \sim \rho^{\pi}, a \sim \pi_{\theta}}[\nabla_{\theta}\log\pi_{\theta}(a|s)Q^{\pi}(s,a)] $$
2.3 Stochastic Actor-Critic Algorithms
- Actor와 Critic이 번갈아가면서 동작하며 stochastic policy를 최적화하는 기법입니다.
- Actor: $Q^{\pi}(s,a)$ 를 근사한 $Q^w(s,a)$ 를 이용해 stochastic policy gradient를 ascent하는 방향으로 policy parameter $\theta$ 를 업데이트함으로써 stochastic policy를 발전시킵니다.
- $\nabla_{\theta}J(\pi_{\theta}) = E_{s \sim \rho^{\pi}, a \sim \pi_{\theta}}[\nabla_{\theta}\log\pi_{\theta}(a|s)Q^{w}(s,a)]$
- Critic: SARSA나 Q-learning같은 Temporal-difference (TD) learning을 이용해 action-value function의 parameter, $w$ 를 업데이트함으로써 $Q^w(s,a)$ 가 $Q^{\pi}(s,a)$ 과 유사해지도록 합니다.
- 실제 값인 $Q^{\pi}(s,a)$ 대신 이를 근사한 $Q^w(s,a)$ 를 사용하게 되면, 일반적으로 bias가 발생합니다. 하지만, compatible condition에 부합하는 $Q^w(s,a)$ 를 사용하게 되면, bias가 발생하지 않습니다.
2.4 Off-policy Actor-Critic
- Distinct behavior policy $\beta(a|s) ( \neq \pi_{\theta}(a|s) )$ 로부터 샘플링된 trajectories 를 이용한 Actor-Critic
- Performance objective function
- $$ J_{\beta}(\pi_{\theta}) = \int_{S}\rho^{\beta}(s)V^{\pi}(s)ds \\ \ \\ = \int_{S}\int_{A}\rho^{\beta}(s)\pi_{\theta}(a|s)Q^{\pi}(s,a)dads $$
- off-policy policy gradient
- $$ \nabla_{\theta}J_{\beta}(\pi_{\theta}) \approx \int_{S}\int_{A}\rho^{\beta}(s)\nabla_{\theta}\pi_{\theta}(a|s)Q^{\pi}(s,a)dads \\ =E_{s \sim \rho^{\beta}, a \sim \beta}[\frac{\pi_{\theta}(a|s)}{\beta_{\theta}(a|s)}\nabla_{\theta}\log\pi_{\theta}(a|s)Q^{\pi}(s,a)] $$
- off-policy policy gradient 식에서의 물결 표시는 Degris, 2012b 논문에 근거합니다.
- Exact off-policy policy gradient 와 이를 approximate 한 policy gradient 는 아래와 같습니다. (빨간색 상자에 있는 항목을 삭제함으로써 근사합니다.)
- [Degris, 2012b] Theorem 1 에 의해 policy parameter 가 approximated policy gradient ( $\nabla_{u}𝑄^{\pi,\gamma}(𝑠,𝑎)$ term 제거)에 따라 업데이트되어도 policy 는 improve 가 됨이 보장되기에 exact off-policy policy gradient 대신 approximated off-policy policy gradient 를 사용해도 괜찮습니다.
- Exact off-policy policy gradient 와 이를 approximate 한 policy gradient 는 아래와 같습니다. (빨간색 상자에 있는 항목을 삭제함으로써 근사합니다.)
- off-policy policy gradient 식에서 $\frac{\pi_{\theta}(a|s)}{\beta_{\theta}(a|s)}$ 는 importance sampling ratio 입니다.
- off-policy actor-critic에서는 $\beta$ 에 의해 샘플링된 trajectory를 이용해서 stochastic policy $\pi$ 를 예측하는 것이기 때문에 importance sampling이 필요합니다.
3. Gradient of Deterministic Policies
3.1 Regularity Conditions
- 어떠한 이론이 성립하기 위한 전제 조건
- Regularity conditions A.1
- $p(s'|s,a), \nabla_{a}p(s'|s,a), \mu_{\theta}(s), \nabla_{\theta}\mu_{\theta}(s), r(s,a), \nabla_{a}r(s,a), p_{1}(s)$ are continuous in all parameters and variables $s, a, s'$ and $x$ .
- regularity conditions A.2
- There exists a $b$ and $L$ such that $\sup_{s}p_{1}(s) < b$ , $\sup_{a,s,s'}p(s'|s,a) < b$ , $\sup_{a,s}r(s,a) < b$ , $\sup_{a,s,s'}\|\nabla_{a}p(s'|s,a)\| < L$ , and $\sup_{a,s}\|\nabla_{a}r(s,a)\| < L$ .
3.2 Deterministic Policy Gradient Theorem
- Deterministic policy
- $\mu_{\theta} : S \to A$ with parameter vector $\theta \in \mathbb{R}^n$
- Probability distribution
- $p(s \to s', t, \mu)$
- Discounted state distribution
- $\rho^{\mu}(s)$
- Performance objective
$$ J(\mu_{\theta}) = E[r^{\gamma}_{1} | \mu] $$
$$ = \int_{S}\rho^{\mu}(s)r(s,\mu_{\theta}(s))ds = E_{s \sim \rho^{\mu}}[r(s,\mu_{\theta}(s))] $$
- DPG Theorem
- MDP 가 A.1 만족한다면, 아래 식이 성립합니다.
- DPG는 state space에 대해서만 평균을 취하면 되기에, state와 action space 모두에 대해 평균을 취해야 하는 SPG에 비해 data efficiency가 좋습니다. 즉, 더 적은 양의 데이터로도 학습이 잘 이뤄지게 됩니다.
3.3 DPG 형태에 대한 informal intuition
- Generalized policy iteration
- 정책 평가와 정책 발전을 한 번 씩 번갈아 가면서 실행하는 정책 iteration
- 위와 같이 해도 정책 평가에서 예측한 가치함수가 최적 가치함수에 수렴합니다.
- 정책 평가와 정책 발전을 한 번 씩 번갈아 가면서 실행하는 정책 iteration
- 정책 평가
- action-value function $Q^{\pi}(s,a)$ or $Q^{\mu}(s,a)$ 을 estimate 하는 것 입니다.
- 정책 발전
- 위 estimated action-value function에 따라 정책을 update하는 것 입니다.
- 주로 action-value function에 대한 greedy maximisation을 사용합니다.
- $\mu^{k+1}(s) = \arg\max\limits_{a}Q^{\mu^{k}}(s,a)$
- greedy 정책 발전은 매 단계마다 global maximization을 해야하는데, 이로 인해 continuous action spaces에서 계산량이 급격히 늘어납니다.
- 그래서 policy gradient 방법이 나옵니다.
- policy 를 $\theta$ 에 대해서 parameterize 합니다.
- 매 단계마다 global maximisation 수행하는 대신, 방문하는 state $s$ 마다 policy parameter를 action-value function $Q$ 의 $\theta$ 에 대한 gradient $\nabla_{\theta}Q^{\mu^{k}}(s,\mu_{\theta}(s))$ 방향으로 proportional하게 update 합니다.
- 하지만 각 state는 다른 방향을 제시할 수 있기에, state distribution $\rho^{\mu}(s)$ 에 대한 기대값을 취해 policy parameter를 update 할 수도 있습니다.
- $\theta^{k+1} = \theta^{k} + \alpha E_{s \sim \rho^{\mu^{k}}} [\nabla_{\theta}Q^{\mu^{k}}(s,\mu_{\theta}(s))]$
- 이는 chain-rule에 따라 아래와 같이 분리될 수 있습니다.
- $\theta^{k+1} = \theta^{k} + \alpha E_{s \sim \rho^{\mu^{k}}} [\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu^{k}}(s,a)\vert_{a=\mu_{\theta}(s)}]$ (7)
- chain rule: $\frac{\partial Q}{\partial \theta} = \frac{\partial a}{\partial \theta} \frac{\partial Q}{\partial a}$
- 하지만 state distribution $\rho^{\mu}$ 은 정책에 dependent 합니다.
- 정책이 바꾸게 되면, 바뀐 정책에 따라 방문하게 되는 state가 변하기 때문에 state distribution이 변하게 됩니다.
- 그렇기에 정책 update 시 state distribution에 대한 gradient를 고려하지 않는데 정책 발전이 이뤄진다는 것은 직관적으로 와닿지 않을 수 있습니다.
- deterministic policy gradient theorem은 state distribution에 대한 gradient 계산없이 위 식(7) 대로만 update해도 performance objective의 gradient를 정확하게 따름을 의미합니다.
3.4 DPG는 SPG의 limiting case
- stochastic policy parameterization
- $\pi_{\mu_{\theta},\sigma}$ by a deterministic policy $\mu_{\theta} : S \to A$ and a variance parameter $\sigma$
- $\sigma = 0$ 이면, $\pi_{\mu_{\theta},\sigma} \equiv \mu_{\theta}$
- Theorem 2. Policy의 variance가 0에 수렴하면, 즉, $\sigma \to 0$ , stochastic policy gradient와 deterministic policy gradient는 동일해집니다.
- 조건: stochastic policy $\pi_{\mu_{\theta},\sigma} = \nu_{\sigma}(\mu_{\theta}(s),a)$
- $\sigma$ 는 variance입니다.
- $\nu_{\sigma}(\mu_{\theta}(s),a)$ 는 condition B.1을 만족합니다.
- MDP는 conditions A.1과 A.2를 만족합니다.
- 결과:
- $\lim\limits_{\sigma\downarrow0}\nabla_{\theta}J(\pi_{\mu_{\theta},\sigma}) = \nabla_{\theta}J(\mu_{\theta})$
- 좌변은 standard stochastic gradient이며, 우변은 deterministic gradient입니다.
- $\lim\limits_{\sigma\downarrow0}\nabla_{\theta}J(\pi_{\mu_{\theta},\sigma}) = \nabla_{\theta}J(\mu_{\theta})$
- 의미:
- deterministic policy gradient는 stochastic policy gradient의 특수 case 입니다.
- 기존 유명한 policy gradients 기법들에 deterministic policy gradients 를 적용할 수 있습니다.
- 기존 기법들 예: compatible function approximation (Sutton, 1999), natural gradients (Kakade, 2001), actor-critic (Bhatnagar, 2007) or episodic/batch methods (Peters, 2005)
- 조건: stochastic policy $\pi_{\mu_{\theta},\sigma} = \nu_{\sigma}(\mu_{\theta}(s),a)$
4. Deterministic Actor-Critic Algorithms
- SARSA critic를 이용한 on-policy actor-critic
- 단점
- deterministic policy에 의해 행동하면 exploration이 잘 되지 않기에, sub-optimal에 빠지기 쉽습니다.
- 목적
- 교훈/정보제공
- 환경에서 충분한 noise를 제공하여 exploration을 시킬 수 있다면, deterministic policy를 사용한다고 하여도 좋은 학습 결과를 얻을 수도 있습니다.
- 예. 바람이 agent의 행동에 영향(noise)을 줌
- Remind: 살사(SARSA) update rule
- $Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) + \alpha(r_{t} + \gamma Q(s_{t+1},a_{t+1}) - Q(s_{t},a_{t}))$
- Algorithm
- Critic은 MSE를 $\bf minimize$ 하는 방향, 즉, action-value function을 stochastic gradient $\bf descent$ 방법으로 update합니다.
- $MSE = [Q^{\mu}(s,a) - Q^{w}(s,a)]^2$
- critic은 실제 $Q^{\mu}(s,a)$ 대신 미분 가능한 $Q^{w}(s,a)$ 로 대체하여 action-value function을 estimate하며, 이 둘 간 mean square error를 최소화하는 것이 목표입니다.
- $\nabla_{w}MSE \approx -2 * [r + \gamma Q^{w}(s',a') - Q^{w}(s,a)]\nabla_{w}Q^{w}(s,a)$
- $\nabla_{w}MSE = -2 * [Q^{\mu}(s,a) - Q^{w}(s,a)]\nabla_{w}Q^{w}(s,a)$
- $Q^{\mu}(s,a)$ 를 $r + \gamma Q^{w}(s',a')$ 로 대체
- $Q^{\mu}(s,a) = r + \gamma Q^{\mu}(s',a')$
- $w_{t+1} = w_{t} + \alpha_{w}\delta_{t}\nabla_{w}Q^{w}(s_{t},a_{t})$
- $w_{t+1} = w_{t} - \alpha_{w}\nabla_{w}MSE$ $\approx w_{t} - \alpha_{w} * (-2 * [r + \gamma Q^{w}(s',a') - Q^{w}(s,a)] \nabla_{w}Q^{w}(s,a)$
- $\delta_{t} = r_{t} + \gamma Q^{w}(s_{t+1},a_{t+1}) - Q^{w}(s_{t},a_{t})$
- $MSE = [Q^{\mu}(s,a) - Q^{w}(s,a)]^2$
- Actor는 식(9)에 따라 보상이$\bf maximize$되는 방향, 즉, deterministic policy를 stochastic gradient $\bf ascent$ 방법으로 update합니다.
- $\theta_{t+1} = \theta_{t} + \alpha_{\theta} \nabla_{\theta}\mu_{\theta}(s_{t})\nabla_{a}Q^{w}(s_{t},a_{t})\vert_{a=\mu_{\theta}(s)}$
- Critic은 MSE를 $\bf minimize$ 하는 방향, 즉, action-value function을 stochastic gradient $\bf descent$ 방법으로 update합니다.
- 단점
- Q-learning 을 이용한 off-policy actor-critic
- stochastic behavior policy $\beta(a|s)$에 의해 생성된 trajectories로부터 deterministic target policy $\mu_{\theta}(s)$ 를 학습하는 off-policy actor-critic입니다
- performance objective
- $J_{\beta}(\mu_{\theta}) = \int_{S}\rho^{\beta}(s)V^{\mu}(s)ds$ $= \int_{S}\rho^{\beta}(s)Q^{\mu}(s,\mu_{\theta}(s))ds$ $= E_{s \sim \rho^{\beta}}[Q^{\mu}(s,\mu_{\theta}(s))]$
- off-policy deterministic policy gradient
- $\nabla_{\theta}J_{\beta}(\mu_{\theta}) = E_{s \sim \rho^{\beta}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu}(s,a)\vert_{a=\mu_{\theta}(s)}]$
- 논문에는 아래와 같이 나와있는데, 물결 표시 부분은 오류로 판단됩니다.
- 근거: Action이 deterministic하기에 stochastic 경우와는 다르게 performance objective에서 action에 대해 평균을 구할 필요가 없습니다. 그렇기에, 곱의 미분이 있을 필요가 없고, [Degris, 2012b]에서 처럼 곱의 미분을 통해 생기는 action-value function에 대한 gradient term을 생략할 필요가 사라집니다.
- $\nabla_{\theta}J_{\beta}(\mu_{\theta}) = E_{s \sim \rho^{\beta}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu}(s,a)\vert_{a=\mu_{\theta}(s)}]$
- Remind: 큐러닝(Q-learning) update rule
- $Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) + \alpha(r_{t} + \gamma \max\limits_{a}Q(s_{t+1},a) - Q(s_{t},a_{t}))$
- algorithm: OPDAC (Off-Policy Deterministic Actor-Critic)
- 살사를 이용한 on-policy deterministic actor-critic과 아래 부분을 제외하고는 같습니다.
- target policy는 $\beta(a|s)$ 에 의해 생성된 trajectories를 통해 학습합니다.
- 업데이트 목표 부분에 실제 행동 값 $a_{t+1}$ 이 아니라 정책으로부터 나온 행동 값 $\mu_{\theta}(s_{t+1})$ 을 사용합니다.
- $\mu_{\theta}(s_{t+1})$ 은 가장 높은 Q 값을 가지는 행동. 즉, Q-learning.
- $\delta_{t} = r_{t} + \gamma Q^{w}(s_{t+1},\mu_{\theta}(s_{t+1})) - Q^{w}(s_{t},a_{t})$
- $w_{t+1} = w_{t} + \alpha_{w}\delta_{t}\nabla_{w}Q^{w}(s_{t},a_{t})$
- $\theta_{t+1} = \theta_{t} + \alpha_{\theta} \nabla_{\theta}\mu_{\theta}(s_{t})\nabla_{a}Q^{w}(s_{t},a_{t})\vert_{a=\mu_{\theta}(s)}$
- 살사를 이용한 on-policy deterministic actor-critic과 아래 부분을 제외하고는 같습니다.
- Stochastic off-policy actor-critic은 대개 actor와 critic 모두 importance sampling을 필요로 하지만, deterministic policy gradient에선 importance sampling이 필요없습니다.
- Actor 는 deterministic 이기에 sampling 자체가 필요없습니다.
- Stochastic policy인 경우, Actor에서 importance sampling이 필요한 이유는 상태 $s$ 에서의 가치 함수 값 $V^{\pi}(s)$ 을 estimate하기 위해 $\pi$ 가 아니라 $\beta$ 에 따라 sampling을 한 후, 평균을 내기 때문입니다.
- 하지만 deterministic policy인 경우, 상태 $s$ 에서의 가치 함수 값 $V^{\pi}(s) = Q^{\pi}(s,\mu_{\theta})$ 즉, action이 상태 s에 대해 deterministic이기에 sampling을 통해 estimate할 필요가 없고, 따라서 importance sampling도 필요없어집니다.
- stochastic vs. deterministic performance objective
- stochastic : $J_{\beta}(\mu_{\theta}) = \int_{S}\int_{A}\rho^{\beta}(s)\pi_{\theta}(a|s)Q^{\pi}(s,a)dads$
- deterministic : $J_{\beta}(\mu_{\theta}) = \int_{S}\rho^{\beta}(s)Q^{\mu}(s,\mu_{\theta}(s))ds$
- Critic이 사용하는 Q-learning은 importance sampling이 필요없는 off policy 알고리즘입니다.
- Q-learning도 업데이트 목표를 특정 분포에서 샘플링을 통해 estimate 하는 것이 아니라 Q 함수를 최대화하는 action을 선택하는 것이기에 위 actor 에서의 deterministic 경우와 비슷하게 볼 수 있습니다.
- Actor 는 deterministic 이기에 sampling 자체가 필요없습니다.
- compatible function approximation 및 gradient temporal-difference learning 을 이용한 actor-critic
- 위 살사/Q-learning 기반 on/off-policy는 아래와 같은 문제가 존재합니다.
- function approximator에 의한 bias
- 일반적으로 $Q^{\mu}(s,a)$ 를 $Q^{w}(s,a)$ 로 대체하여 deterministic policy gradient를 구하면, 그 gradient는 ascent하는 방향이 아닐 수도 있습니다.
- off-policy learning에 의한 instabilities
- function approximator에 의한 bias
- 그래서 stochastic처럼 $\nabla_{a}Q^{\mu}(s,a)$ 를 $\nabla_{a}Q^{w}(s,a)$ 로 대체해도 deterministic policy gradient에 영향을 미치지 않을 compatible function approximator $Q^{w}(s,a)$ 를 찾아야 합니다.
- Theorem 3. 아래 두 조건을 만족하면, $Q^{w}(s,a)$ 는 deterministic policy $\mu_{\theta}(s)$ 와 compatible 합니다. 즉, $\nabla_{\theta}J_{\beta}(\mu_{\theta}) = E_{s \sim \rho^{\beta}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{w}(s,a)\vert_{a=\mu_{\theta}(s)}]$
- $\nabla_{a}Q^{w}(s,a)\vert_{a=\mu_{\theta}(s)} = \nabla_{\theta}\mu_{\theta}(s)^{\top}w$ 입니다.
- $w$ 는 $MSE(\theta, w) = E[\epsilon(s;\theta,w)^{\top}\epsilon(s;\theta,w)]$ 를 최소화합니다.
- $\epsilon(s;\theta,w) = \nabla_{a}Q^{w}(s,a)\vert_{a=\mu_{\theta}(s)} - \nabla_{a}Q^{\mu}(s,a)\vert_{a=\mu_{\theta}(s)}$
- Theorem 3은 on-policy 뿐만 아니라 off-policy에도 적용 가능합니다.
- $Q^{w}(s,a) = (a-\mu_{\theta}(s))^{\top}\nabla_{\theta}\mu_{\theta}(s)^{\top} w + V^{v}(s)$
- 어떠한 deterministic policy에 대해서도 위 형태와 같은 compatible function approximator가 존재합니다.
- 앞의 term은 advantage를, 뒤의 term은 value로 볼 수 있습니다.
- $Q^{w}(s,a) = \phi(s,a)^{\top} w + v^{\top}\phi(s)$
- 정의 : $\phi(s,a) \overset{\underset{\mathrm{def}}{}}{=} \nabla_{\theta}\mu_{\theta}(s)(a-\mu_{\theta}(s))$
- 일례 : $V^{v}(s) = v^{\top}\phi(s)$
- Theorem 3 만족 여부
- 첫 번째 조건 만족합니다.
- 두 번째 조건은 대강 만족합니다.
- $\nabla_{a}Q^{\mu}(s,a)$ 에 대한 unbiased sample을 획득하기는 매우 어렵기에, 일반적인 정책 평가 방법들로 $w$ 를 학습합니다.
- 이 정책 평가 방법들을 이용하면 $Q^{w}(s,a) \approx Q^{\mu}(s,a)$ 인 reasonable solution을 찾을 수 있기에 대강 $\nabla_{a}Q^{w}(s,a) \approx \nabla_{a}Q^{\mu}(s,a)$ 이 될 것입니다.
- action-value function에 대한 linear function approximator는 큰 값을 가지는 actions에 대해선 diverge할 수 있어 global하게 action-values 예측하기에는 좋지 않지만, local critic에 사용할 때는 매우 유용합니다.
- 즉, 절대값이 아니라 작은 변화량을 다루는 gradient method 경우엔 $A^{w}(s,\mu_{\theta}(s)+\delta) = \delta^{\top}\nabla_{\theta}\mu_{\theta}(s)^{\top}w$ 로, diverge하지 않고, 값을 얻을 수 있습니다.
- COPDAC-Q algorithm (Compatible Off-Policy Deterministic Actor-Critic Q-learning critic)
- Critic: 실제 action-value function에 대한 linear function approximator인 $Q^{w}(s,a) = \phi(s,a)^{\top}w$ 를 estimate합니다.
- $\phi(s,a) = a^{\top}\nabla_{\theta}\mu_{\theta}$
- Behavior policy $\beta(a|s)$ 로부터 얻은 samples를 이용하여 Q-learning이나 gradient Q-learning과 같은 off-policy algorithm으로 학습 가능합니다.
- Actor: estimated action-value function에 대한 gradient를 $\nabla_{\theta}\mu_{\theta}(s)^{\top}w$ 로 치환 후, 정책을 업데이트합니다.
- $\delta_{t} = r_{t} + \gamma Q^{w}(s_{t+1},\mu_{\theta}(s_{t+1})) - Q^{w}(s_{t},a_{t})$
- $w_{t+1} = w_{t} + \alpha_{w}\delta_{t}\phi(s_{t},a_{t})$
- $\theta_{t+1} = \theta_{t} + \alpha_{\theta} \nabla_{\theta}\mu_{\theta}(s_{t})(\nabla_{\theta}\mu_{\theta}(s_{t})^{\top} w_{t})$
- Critic: 실제 action-value function에 대한 linear function approximator인 $Q^{w}(s,a) = \phi(s,a)^{\top}w$ 를 estimate합니다.
- off-policy Q-learning은 linear function approximation을 이용하면 diverge 할 수도 있습니다.
- $\mu_{\theta}(s_{t+1})$ 이 diverge할 수도 있기 때문으로 판단됩니다.
- 그렇기에 simple Q-learning 대신 다른 기법이 필요합니다.
- 그렇기에 critic 에 gradient Q-learning 사용한 COPDAC-GQ (Gradient Q-learning critic) algorithm을 제안합니다.
- gradient temporal-difference learning에 기반한 기법들은 true gradient descent algorithm이며, converge가 보장됩니다. (Sutton, 2009)
- 기본 아이디어는 stochastic gradient descent로 mean-squared projected Bellman error (MSPBE)를 최소화하는 것입니다.
- critic이 actor보다 빠른 time-scale로 update되도록 step size들을 잘 조절하면, critic은 MSPBE를 최소화하는 parameters로 converge하게 됩니다.
- critic에 gradient temporal-difference learning의 일종인 gradient Q-learning을 사용한 논문입니다. (Maei, 2010)
- gradient temporal-difference learning에 기반한 기법들은 true gradient descent algorithm이며, converge가 보장됩니다. (Sutton, 2009)
- COPDAC-GQ algorithm
- $\delta_{t} = r_{t} + \gamma Q^{w}(s_{t+1},\mu_{\theta}(s_{t+1})) - Q^{w}(s_{t},a_{t})$
- $\theta_{t+1} = \theta_{t} + \alpha_{\theta} \nabla_{\theta}\mu_{\theta}(s_{t})(\nabla_{\theta}\mu_{\theta}(s_{t})^{\top} w_{t})$
- $w_{t+1} = w_{t} + \alpha_{w}\delta_{t}\phi(s_{t},a_{t}) - \alpha_{w}\gamma\phi(s_{t+1}, \mu_{\theta}(s_{t+1}))(\phi(s_{t},a_{t})^{\top} u_{t})$
- $v_{t+1} = v_{t} + \alpha_{v}\delta_{t}\phi(s_{t}) - \alpha_{v}\gamma\phi(s_{t+1})(\phi(s_{t},a_{t})^{\top} u_{t})$
- $u_{t+1} = u_{t} + \alpha_{u}(\delta_{t}-\phi(s_{t}, a_{t})^{\top} u_{t})\phi(s_{t}, a_{t})$
- stochastic actor-critic과 같이 매 time-step 마다 update 시 필요한 계산의 복잡도는 $O(mn)$ 입니다.
- m은 action dimensions, n은 number of policy parameters
- Natural policy gradient를 이용해 deterministic policies를 찾을 수 있습니다.
- $M(\theta)^{-1}\nabla_{\theta}J(\mu_{\theta})$ 은 any metric $M(\theta)$ 에 대한 performance objective (식(14))의 steepest ascent direction 입니다. (Toussaint, 2012)
- Natural gradient는 Fisher information metric $M_{\pi}(\theta)$ 에 대한 steepest ascent direction 입니다.
- $M_{\pi}(\theta) = E_{s \sim \rho^{\pi}, a \sim \pi_{\theta}}[\nabla_{\theta}\log\pi_{\theta}(a|s)\nabla_{\theta}\log\pi_{\theta}(a|s)^{\top}]$
- Fisher information metric은 policy reparameterization에 대해 불변입니다. (Bagnell, 2003)
- deterministic policies에 대한 metric으로 $M_{\mu}(\theta) = E_{s \sim \rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{\theta}\mu_{\theta}(s)^{\top}]$ 을 사용합니다.
- 이는 variance가 0인 policy에 대한 Fisher information metric으로 볼 수 있습니다.
- $\frac{\nabla_{\theta}\pi_{\theta}(a\vert s)}{\pi_{\theta}(a\vert s)}$에서 policy variance가 0이면, 특정 s에 대한 $\pi_{\theta}(a|s)$만 1이 되고, 나머지는 0입니다.
- deterministic policy gradient theorem과 compatible function approximation을 결합하면 $\nabla_{\theta}J(\mu_{\theta}) = E_{s \sim \rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{\theta}\mu_{\theta}(s)^{\top}w]$ 이 됩니다.
- $\nabla_{\theta}J(\mu_{\theta}) = E_{s \sim \rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu}(s,a)\vert_{a=\mu_{\theta}(s)}]$
- $\nabla_{a}Q^{\mu}(s,a)\vert_{a=\mu_{\theta}(s)} \approx \nabla_{a}Q^{w}(s,a)\vert_{a=\mu_{\theta}(s)} = \nabla_{\theta}\mu_{\theta}(s)^{\top}w$
- 그렇기에 steepest ascent direction은 $M_{\mu}(\theta)^{-1}\nabla_{\theta}J_{\beta}(\mu_{\theta}) = w$ 이 됩니다.
- $E_{s \sim \rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{\theta}\mu_{\theta}(s)^{\top}]^{-1}E_{s \sim \rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{\theta}\mu_{\theta}(s)^{\top}w] = w$
- 이 알고리즘은 COPDAC-Q 혹은 COPDAC-GQ에서 $\theta_{t+1} = \theta_{t} + \alpha_{\theta} \nabla_{\theta}\mu_{\theta}(s_{t})(\nabla_{\theta}\mu_{\theta}(s_{t})^{\top} w_{t})$ 식을 $\theta_{t+1} = \theta_{t} + \alpha_{\theta}w_{t}$ 로 바꿔주기만 하면 됩니다.
- 위 살사/Q-learning 기반 on/off-policy는 아래와 같은 문제가 존재합니다.
5. Experiments
5.1. Continuous Bandit
- Stochastic Actor-Critic (SAC)과 COPDAC 간 성능 비교 수행합니다.
- Action dimension이 커질수록 성능 차이가 심합니다.
- 빠르게 수렴하는 것을 통해 DPG의 data efficiency가 SPG에 비해 좋다는 것을 확인할 수 있지만, 반면, time-step이 증가할수록 SAC와 COPDAC 간 성능 차이가 줄어드는 것을 통해 성능 차이가 심하다는 것은 일정 time step 내에서만 해당하는 것이라고 유추해볼 수 있습니다.

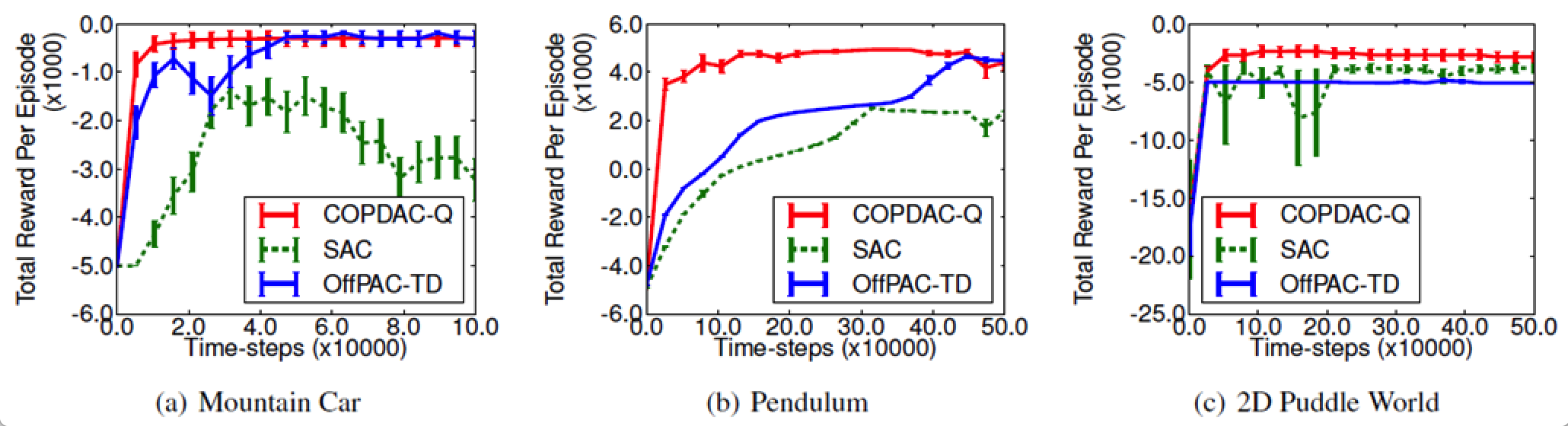
5.2. Continuous Reinforcement Learning
- COPDAC-Q, SAC, off-policy stochastic actor-critic(OffPAC-TD) 간 성능 비교 수행합니다.
- COPDAC-Q의 성능이 약간 더 좋습니다.
- COPDAC-Q의 학습이 더 빨리 이뤄집니다.
5.3. Octopus Arm
- 목표: 6 segments octopus arm (20 action dimensions & 50 state dimensions)을 control하여 target을 맞추는 것입니다.
- COPDAC-Q 사용 시, action space dimension이 큰 octopus arm을 잘 control하여 target을 맞춥니다.

- 기존 기법들은 action spaces 혹은 action과 state spaces 둘 다 작은 경우들에 대해서만 실험했다고 하며, 비교하고 있지 않습니다.
- 기존 기법들이 6 segments octopus arm에서 동작을 잘 안 했을 것 같긴한데, 그래도 실험해서 보여줬으면 하지만 실험을 하지 않았습니다.
- 8 segment arm 동영상이 저자 홈페이지에 있다고 하는데, 안 보입니다.
- COPDAC-Q 사용 시, action space dimension이 큰 octopus arm을 잘 control하여 target을 맞춥니다.
- [참고] Octopus Arm 이란?

'프로젝트 > 피지여행' 카테고리의 다른 글
| 6. Trust Region Policy Optimization (0) | 2023.03.08 |
|---|---|
| 5. Natural Policy Gradient (0) | 2023.03.06 |
| 4. Deep Deterministic Policy Gradient (DDPG) (0) | 2023.03.06 |
| 2. Policy Gradient Methods for Reinforcement Learning with Function Approximation (0) | 2023.03.05 |
| 1. PG Travel Guide (0) | 2023.02.21 |


