Author: 이승현
Date: February 13, 2019
Inverse RL 5번째 논문

- Author : Jonathan Ho, Stefano Ermon
- Paper Link : https://papers.nips.cc/paper/6391-generative-adversarial-imitation-learning.pdf
- Proceeding : Advances in Neural Information Processing Systems (NIPS) 2016
0. Abstract
전문가의 시연으로부터 policy를 학습하는 문제를 해결하기 위해 사용되는 대표적인 imitation learning 방법으로는 먼저 inverse reinforcement learning으로 cost fuction을 복원하고, 이 cost function과 reinforcement learning을 활용하여 policy를 학습하는 두 단계의 알고리즘이 있습니다. 하지만 이는 목적에 비해 과정이 직접적이지 않으며 매우 느립니다. 이에 이 논문에서는 imitation learning과 generative adversarial networks의 유사점에서 착한하여, data로 부터 직접적으로 policy를 학습하는 일반적인 framework를 제안합니다. 그리고 크고 고차원의 환경에서 행해진 복잡한 expert의 행동에도 잘 적용가능한것을 보임으로서 알고리즘의 성능을 입증하고자 합니다.
- 이후 본문에서는 더 확실한 이해를 위해 논문의 저자인 Stefano Ermon이 Toyota에서 이 논문에 대해 강의한 슬라이드를 figure로 자주 인용하겠습니다.
- 강의 링크 : https://youtu.be/bcnCo9RxhB8
1. Introduction
Imitation Learning(IL) 은 Expert의 시연으로부터 어떻게 행동하는지를 학습하는 문제로서, learner는 시연된 trajectory만을 보고 학습할 뿐이며 학습 중엔 추가적인 데이터를 받지 않습니다. IL에는 대표적으로 Behavioral clonong과 Inverse Reinforcement Learning 이라는 두 가지 접근 방식이 있습니다.
Behavioral cloning(BC) 은 Supervised learning 방식으로 expert의 시연을 학습하는 것을 말합니다. 때문에 학습을 위한 데이터가 많아야 하며 경로가 지날수록 오차가 누적되어 나중엔 크게 달라지는 문제가 있습니다.

Inverse reinforcement learning(IRL) 은 Expert의 시연이 가장 좋은 성능을 갖도록 하는 cost function 을 추정하는 일종의 estimation 문제를 말합니다. BC처럼 learner의 매 경로를 expert의 경로와 일치시키려는 과정이 없으므로 오차가 누적되는 문제가 없어 전체 경로 최적화 혹은 경로 예측 문제에 효과적입니다.

- cost function은 reward function과 유사한 개념으로서 클수록 좋은 reward function과 달리 작을수록 좋다는 차이점이 있습니다. 제어공학, 산업공학에서 다루는 비용 함수와도 최적화 측면에서 같은 개념입니다.
IRL 알고리즘은 내부적으로 reinforcement learning loop를 가지고 있어 매우 비효율적입니다. 하지만 cost function을 학습하며, expert의 직접적인 행동을 배우는게 아니라 행동의 의도(explains expert behavior)를 학습한다는 특징을 가지고 있습니다. 여기서 "Learner의 학습 목적이 expert의 행동을 모방하고자 하는것이라면 굳이 비효율적으로 많은 연산을 들여 cost function을 배울 필요가 있는가?" 라는 의문이 듭니다. 이러한 의문에서 시작하여, 이 논문(이하 GAIL)의 저자는 policy를 바로 학습하는 효율적인 알고리즘을 제시합니다.
2. Background
2.1 Preliminaries
본문에 들어가기 앞서 GAIL에서 다루는 기호들을 먼저 살펴보겠습니다. $\overline { \mathbb{R} }$ 은 확장된 실수로서 실수의 집합에 양의 무한대와 음의 무한대가 포함된걸 의미합니다. 즉, $\mathbb{R}\cup { \infty }$ 를 뜻합니다. $\Pi$는 주어진 상태 $\mathcal{S}$에서 행동 $\mathcal{A}$를 선택하는 Stationary 한 stochastic policy의 집합을 의미합니다. 이렇게 주어진 상태 $s$와 행동$a$으로부터 다음 상태 $s'$는 dynamics model $P( s'| s, a)$ 로 부터 도출됩니다. $\mathbb{E_{\pi}}{[c(s,a)]},\triangleq,\mathbb{E}{[\sum_{t=0}^{\infty}\gamma^t c(s_t,a_t)]}$는 policy $\pi\in\Pi$ 의 cost function에 대한 기대값으로, $\gamma$-discount된 infinite horizon 공간에서 $\pi$가 생성한 경로에 대한 cost function의 기대값을 의미합니다. ${\pi}_E$ 는 expert의 policy를 의미합니다.
2.2 Inverse reinforcement learning
IRL은 행동의 의도를 학습하는 특징이 있다고 앞서 언급하였습니다. 즉 Expert의 policy ${E}_{\pi}$가 주어졌을때 이를 IRL을 사용하여 설명할 수 있습니다. 특히 GAIL에서는 아래의 maximum causal entropy IRL를 사용하였으며 이에 대한 해가 있다고 가정합니다.
$$
\underset { c\in { C } }{\mathbf{maximize} }(\min_{\pi\in\Pi}-H( \pi )+ { \mathbb{E_{\pi}}[ c(s,a)] })- { \mathbb{E_{\pi_E}}}[c(s,a)]
$$
이때 $H(\pi)\triangleq\mathbb{E_{\pi}}[ \log{\pi(a|s)} ]$ 는 policy $\pi$에 대한 $\gamma$-discounted causal entropy입니다. 실제 계산에선 $\pi_{E}$는 시연된 몇개의 trajectory로 주어지므로 이로부터 $\pi_{E}$의 cost에 대한 기대값을 구합니다.
위 Maximum causal entropy IRL식을 해석하자면 expert의 policy에는 낮은 값을 주면서, 다른 policy엔 높은 값을 주는 cost function을 구한 뒤 이를 reinforcement learning 과정에서 cost를 낮추는 더 나은 policy를 다시 구하는 반복과정을 의미합니다. Reinforcement learning 과정만 따로 본다면 다음과 같습니다.
$$
\mathbf{RL}(c)=\underset{\pi\in\Pi}{\mathbf{argmin}}-H(\pi)+{ \mathbb{E} }_{ \pi }[ c(s,a) ]
$$
이는, 누적된 cost를 최소화 하는 동시에 높은 entropy를 갖는 policy를 찾는 것을 의미합니다. MaxEnt IRL에서 다뤘던 바와 같이, cost가 0이 되는 등의 여러 개의 policy가 해가 되는 ill-posed 상황을 막기위해 regularize term으로서 Maximize Entropy 방법을 사용하였습니다.

지금까지 설명한 IRL 알고리즘을 저자는 아래와 같이 요약하였습니다.

하지만 이러한 IRL 방식은 앞서 Introduction에서 언급한 두 가지 큰 문제점을 가지고 있습니다. 첫번째는 Indirect문제로 구하고자 하는건 policy이지만 cost를 거쳐서 구한다는 점과, 두번째는 Expensive문제로 알고리즘 내부의 RL Loop가 매우 비효율적이라는 점입니다. 이제 기존의 정의들을 새롭게 조합하여 이 문제들을 하나씩 해결해보겠습니다.
3. Characterizing the induced optimal policy
Gaussian process 및 Neural network와 같이 복잡한 function approximator 를 cost function으로 사용하면, expert의 행동을 feature를 하나하나 선정해주는 일 없이 더 잘 표현할 수 있습니다. 하지만 이러한 복잡한 cost function을 학습하기에는 보통 주어진 expert의 시연 dataset이 매우 부족하므로 쉽게 over fitting 되버리고 맙니다. 때문에 데이터의 범위를 확장하고자 실수 전구간에서 정의되는 convex cost function regularizer $\psi:{\mathbb{R}}^{\mathcal{S}\times\mathcal{A}}\rightarrow\overline { \mathbb{R} }$를 도입합니다. 이 $\psi$는 이후 논의될 내용에서 중요한 역할을 할것입니다.
저자와 유사한 방법을 Finn. et al (https://arxiv.org/pdf/1603.00448.pdf) 에서도 사용했는데, 마찬가지로 IRL에 regularizer를 사용하였으며 그 형태만 다를 뿐입니다. 자세한 내용은 Finn 교수님의 강의를 참고하시길 바랍니다. (https://www.youtube.com/watch?v=d9DlQSJQAoI)
이제 $\psi$를 사용하여 IRL 과정을 두 단계로 다시 써보겠습니다.
1. 시연으로 부터 cost function을 구하는 단계
$$
{\mathbf{IRL_{\psi}}}(\pi_E)=\underset { c\in { {\mathbb{R}}^{\mathcal{S}\times\mathcal{A}} } }{\mathbf{argmax} }-\psi(c)+( \min_{ \pi\in\Pi }{ -H( \pi ) + { \mathbb{E_{\pi}} }[ c(s,a) ] } ) - { \mathbb{E_{\pi_E}} }[c(s,a)]
$$
2. RL로 cost function에 대한 optimal policy를 구하는 단계
$$
\mathbf{RL}(c)=\underset{\pi\in\Pi}{\mathbf{argmin}}-H(\pi)+{ \mathbb{E} }_{ \pi }[ c(s,a) ]
$$
이제 이 두 단계를 합쳐 중간과정 없이 직접적으로 polciy를 구하는 방법을 찾아보겠습니다. 다시말해 주어진 expert의 시연 $\pi_E$에 대한 두 최적화 단계의 합성인 $\mathbf{RL}\circ\mathbf{IRL}_{\psi}(\pi_E)$를 구하는 방법을 찾습니다.

이를 하려면, 다른 방법으로 최적화 문제을 표현할 필요가 있습니다. 먼저 "occupancy measure" 이라는 새로운 개념을 도입하겠습니다. occupancy measure은 policy $\pi$에 대한 state-action의 탐색적 점유분포로서, 다음과 같이 정의합니다.
$$
\rho_{\pi}:\mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R} ;as; \rho_{\pi}(s,a) = \pi(a|s)\sum_{t=0}^{\infty}\gamma^tP(s_t=s|\pi)
$$
이는 식 그대로 policy를 시행했을 때, 각 state-action pair에 대한 방문 확률을 구한 것입니다. 이 개념을 활용하면, IRL 및 RL과정 모두에 포함되어있는 policy에 대한 cost의 기대값도 다음과 같이 새롭게 정의 할 수 있습니다.
$$
\mathbb{E_{\pi}}[c(s,a)]=\sum_{s,a}\rho_{\pi}(s,a)c(s,a)
$$
마지막으로 conjugate function이라는 개념을 알아야 하는데, 생소하신 분은 박진우님의 ‘모두를 위한 컨벡스 최적화’(https://wikidocs.net/21001)를 참고바랍니다. Conjugate function은 기하학적으로 선형함수 $y^Tx$ 와 $f(x)$ 간의 maximum gap을 의미하지만 이는 여기서 중요한건 아니고 식의 형태가 다음과 같다는 점과 convex(affine) 함수 $y$의 pointwise maximum 이므로 conjugate function이 항상 convex라는 사실 두 가지만 기억하면 됩니다.
$$
f^*(x)=\sup_{y\in\mathbb{R}^{\mathcal{S}\times\mathcal{A}}}x^Ty-f(y)
$$
이를 종합하여 저자는 RL과 IRL의 합성을 변형하여 새로운 optimization problem을 다음과 같이 제시합니다.
$$
\mathbf{RL}\circ\mathbf{IRL_{\psi}}(\pi_E)=\underset{\pi \in \Pi}{\mathbf{argmin}}-H(\pi)+\psi^*(\rho_{\pi}-\rho_{\pi_E})
$$

여기서 cost regularizer $\psi$의 conjugate function을 사용한 $\psi^*(\rho_{\pi}-\rho_{\pi_E})$는 learner의 현재 policy에 대한 점유 분포가 expert의 분포와 얼마나 가까운지를 의미합니다. 갑자기 나타난 합성형태에 어리둥절 할 수 있겠지만, 자세한 증명(Appendix A.1) 보다는 실제 예를 들어 설명을 해보겠습니다.
참고로 $\psi$를 어떻게 정하느냐에따라 다양한 imitation learning이 될수 있으며, 이 논문에선 상수함수인 경우, indicator function을 사용한 경우(App), 단점들을 보완한 새로운 제안(GAIL)을 다룰 것임을 빠른 이해를 위해 미리 말씀드립니다.
먼저 cost regularizer $\psi$로 상수 함수를 사용한 경우입니다. 상수함수는 optimization에 아무런 영향이 없으므로 다시말해 cost regularization을 하지 않은 경우 어떤 결과가 나타나는지를 몇가지 Lemma들을 활용하여 유도해보겠습니다.
이에 앞서 policy 집합 $\Pi$로 부터 나타날 수 있는 유효한 occupancy measure의 집합을 $\mathcal{D}\triangleq { \rho_{\pi}:\pi\in\Pi}$ 라고 쓰겠습니다. 이 때, $\Pi$와 $\mathcal{D}$는 1대1 대응관계입니다. 유도를 위한 첫번째 Lemma 입니다.
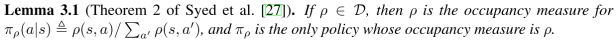
여기선 1대1 대응관계임을 바탕으로 occupancy measure $\rho\in\mathcal{D}$로 부터 $\pi_{rho}$를 정의하였습니다. 또한 occupancy measure $\rho$가 있을 때 $\pi_{\rho}$는 이에 대한 유일한 policy라고 정의합니다. 다음은 유도를 위한 두번째 Lemma입니다.

여기선 policy가 아니라 occupancy measure에 대한strictly concave한 causal entropy $\overline{H}_{\rho}$를 정의하였습다. 그리고 policy와 이에 해당하는 occupancy measure의 Entropy가 같으며, 반대로 occupancy measure과 이에 해당하는 policy의 Entropy가 같음을 정의하였습니다. 요약하자면 Lemma 3.1과 3.2는 policy와 occupancy measure이 서로 제약없이 교체 가능하능함을 의미합니다. 이제 이 중요한 성질을 사용하여 아래의 새로운 Lemma를 설명해보겠습니다.

이 Lemma 부터는 본격적으로 duality에 대해 다루고 있으며 기존의 optimization 문제를 어떻게 새로운 optimization으로 표현할지에 대해 접근합니다. 그러려면 먼저 Lagrangian부터 알아야 하는데, 생소하신 분은 마찬가지로 박진우 님의 모두의 컨벡스 최적화를 참고부탁드립니다.
- Lagrangian 의 정의 (https://wikidocs.net/20579) : primal problem을 선형 조합하여 새로운 Lagrangian이라는 objective 를 만듬.
- Lagrange dual function (https://wikidocs.net/20583) : Lagrange dual function은 primal optimal 의 lower bond로서 항상 같거나 작다.
- Lagrange dual problem (https://wikidocs.net/20584) : Lagrange dual problem은 primal problem이 convex가 아니더라도 항상 concave (convex optimization problem).
- Strong duality (https://wikidocs.net/20585) : primal problem이 convex이고 strictly feasible한 solution이 하나 이상 있으면 strong duality라고 하며, 이때 primal optimal = dual optimal 이 성립함.

다시말해 위의 primal convex function과 아래의 dual concave의 optimal point가 일치함을 뜻함.
이제 다시한번 더 Lemma 3.3을 봅시다.

여기선 Lemma 3.1, 3.2를 활용하여 policy에 대한 Lagrangian과 occupancy measure에 대한 Lagrangian을 정희 한 후, 앞서와 마찬가지로 policy와 이에 해당하는 occupancy measure의 Lagrangian이 같으며, 반대로 occupancy measure과 이에 해당하는 policy의 Entropy의 Lagrangian이 같음을 정의하였습니다. 모든 lemma를 설명하였으므로 이제 드디어 cost regularizer가 상수인 경우를 이야기 해볼 수 있습니다.

즉, $\psi$가 상수일 경우엔 learner와 expert의 occupancy measure이 정확히 같아집니다. 이에 대한 증명을 아래와 같이 설명합니다.


다시말해 새롭게 정의한 occupancy measure의 Lagrangian과 앞서 occupancy measure을 사용하여 정의한 cost의 expectation을 사용하면 IRL단계의 식을 간단하게 Lagrangian dual problem의 형태로 표현이 가능합니다(6번식). 이를 통해 Lagrangian의 정의에 따라 Primal problem이 7번식과 같음을 알 수 있습니다. 즉, 앞서 무슨 의미인지 와닿지 않았던 Proposition 3.1에서 cost regularizer가 상수인 형태가 되는것입니다.
여기서 모두의 컨벡스 최적화에서 다룬 내용과 Lemma들을 더 살펴보면, 앞서 새롭게 정의한 occupancy measure의 Entropy가 strictly concave (=convex)라고 했으며, IRL solution이 존재한다고 가정하였으므로, 이는 strong duality를 만족한다고 할 수 있으며, 따라서 dual optimal $\tilde { c }$와 primal optimal $\tilde { \rho }$가 서로 유일하게 구할수 있게 됩니다. 즉,
$$
\tilde{\rho}=\underset{\rho\in\mathcal{D}}{\mathbf{argmin}}\overline{L}(\rho,\tilde{c})=\underset{\rho\in\mathcal{D}}{\mathbf{argmin}}-\overline{H}(\rho)+\sum_{(s,a)}{\tilde{c}(s,a)\rho(s,a)}=\rho_E
$$
입니다. 이때 마지막 등호는 primal problem의 constraints $\rho(s,a)=\rho_{E}(s,a)$ 로부터 구할 수 있습니다. 여기에 optimal cost $\tilde{c}$로부터 optimal policy $\tilde{\pi}\in\mathbf{RL}(\tilde{c})$가 구해지고 이에 해당하는 occupancy measure $\rho_{\tilde{\pi}}$가 있다면 다음이 성립합니다.
$$
\rho_{\tilde{\pi}}=\tilde{\rho}=\rho_E
$$
이로서 cost regularizer로 상수함수를 사용하는 경우에 대한 아래의 Proposition 3.2가 증명 되었습니다.

여기까지 내용을 요약하면 IRL을 Primal인 RL과 dual인 cost로 나누어 dual ascent를 하기엔 primal인 RL 비효율적이라 적합하지 않으므로, IRL을 occupancy measure matching이라는 primal 문제의 dual로 바꾸어 효율적으로 최적화를 하는것입니다. 이에 대해 저자는 다음과 같이 정리합니다.

4. Practical occupancy measure matching
앞서 section.3에서는 상수 regularizer를 사용할 경우 expert와 정확히 일치하는 occupancy measure를 구할 수 있다는 것을 확인하였습니다. 하지만 이를 실제로 사용하는것엔 문제가 많습니다. 실제 환경은 large envrionment인 경우가 대부분입니다. 때문에 expert sample을 아무리 많이 구하려고해도 결국 모든 state및 action을 경험할 수 없으므로 데이터의 정보가 제한적입니다. 때문에 정확한 occupancy measure의 matching을 통한 policy의 학습은
- 첫번째로 expert가 방문하지 않은 $(s,a)$ 페어는 learner도 하지 못하는 확장성의 제한이 생깁니다.
- 두번째로 large environment에서 policy approximator $\theta$를 사용할 때, 수많은 $(s,a)$ 페어 만큼의 constraints가 생기는 문제가 생깁니다.
상수 regularizer의 문제점을 피하고자 이번엔 상수 cost regularizer 를 사용한 7번식에 occupancy measure 분포의 차이에 따라 smoothly penalizing을 하는 regularizer $d_{\psi}(\rho_{\pi},\rho_E)\triangleq{\psi}^*(\rho_{\pi},\rho_E)$를 아래와 같이 추가해봅시다.
$$
\underset{\pi}{\mathbf{minimize}},d_{\psi}(\rho_{\pi},\rho_E)-H(\pi)\qquad\qquad(8)
$$
4.1 Entropy-regularized apprenticeship learning
이제 앞서 다룬 IRL논문중에 하나인 Apprenticeship Learning via Inverse Reinforcement Learning (이하 APP) 알고리즘을 떠올려 봅시다.
$$
\underset{\pi}{\mathbf{minimize}}\max_{c\in\mathcal{C}}\mathbb{E_{\pi}}[c(s,a)]-\mathbb{E_{\pi_E}}[c(s,a)]\qquad\qquad(9)
$$
APP 알고리즘은 reward function (여기서는 cost function)을 기저함수인 $f_1,\dots,f_d(s,a)$의 선형조합의 집합인 $\mathcal{C}_{linear}$ 에서 찾았으며, optimization에 feature expectation matching과 $l_2$ constraint를 사용하였습니다.

이제 Section.3에서 정의한 ${\mathbb{E_{\pi}}}[c(s,a)]=\sum_{s,a}{\rho_\pi(s,a)c(s,a)}$를 9번식 APP에 대입합니다. 그리고 cost set에서는 0, 그 외에서는 $+\infty$인 indicator function $\delta_{\mathcal{C}}:{\mathbb{R}}^{\mathcal{S}\times\mathcal{A}}\rightarrow\overline { \mathbb{R} }$를 cost regularizer로 추가합니다. 그럼 놀랍게도 APP는 다음과 같이 indicator function의 conjugate function $\delta_{\mathcal{C}}^*$에 learning와 expert의 occupancy measure을 대입한 형태가 됩니다.
$$
\max_{c\in\mathcal{C}}\mathbb{E_{\pi}}[c(s,a)]-\mathbb{E_{\pi_E}}[c(s,a)]\ =\max_{c\in\mathbb{R}^{\mathcal{S}\times\mathcal{A}}}-\delta_{\mathcal{C}} + \sum_{s,a}(\rho_{\pi}(s,a)-\rho_{\pi_E}(s,a))c(s,a)\ \ =\ \ \delta_c^*(\rho_{\pi}-\rho_{\pi_E})
$$
마지막으로 위 8번식에서 $d_{\psi}(\rho_{\pi},\rho_E)$를 $\delta_{\mathcal{C}}^(\rho_{\pi}-\rho_{\pi_E})$ 치환하면,
다음의 *entropy-regularized apprenticeship learning** 알고리즘이 완성됩니다.
$$
\underset{\pi}{\mathbf{minimize}}-H(\pi)+\max_{c\in\mathcal{C}}\mathbb{E_{\pi}}[c(s,a)]-\mathbb{E_{\pi_E}}[c(s,a)]\qquad\qquad(11)
$$
이로서 cost regularizer로 indicator fuction $\delta_{\mathcal{C}}$ 를 사용하는것이 곧 APP에 Entropy regularizer $H(\pi)$를 추가하는것과 동일하다는것을 알게 되었습니다. Cost regularizer로 indicator fuction사용하는 APP에도 여전히 문제가 있습니다. 물론 상수 함수를 사용할때와는 달리 이젠 large envrionment에도 적용이 가능해졌습니다. 하지만 APP는 function basis의 선형조합으로 cost fuction을 표현하므로 expert가 복잡한 의도를 담고 있을경우 cost fuction이 이를 충분히 반영했다고 보장하기가 어렵습니다. 결과적으로 cost function의 제한이 없는 새로운 cost regularizer가 필요해지게 됩니다.

5. Generative adversarial imiation learning
이전 세션까지 RL과 IRL의 문제를 아래와 같이 expert E의 occupancy measure 와 유사한 policy를 찾는 문제로 정의하였습니다.
$$
\mathbf{RL}\circ\mathbf{IRL_{\psi}}(\pi_E)=\underset{\pi \in \Pi}{\mathbf{argmin}}-H(\pi)+\psi^*(\rho_{\pi}-\rho_{\pi_E})
$$
그리고 regularizer $\psi$를 다양하게 선택함으로서 imitation learning의 특성을 바꿀 수 있다는것을 확인하였습니다. 그 결과 상수 regularizer를 사용할 경우 정확히 일치하는 occupancy meaure를 찾을 순 있지만 large envrionment에서는 사용하지 못하는것을 확인하였고, indicator regularizer를 사용할 경우 large envirionment에서 사용하능하지만 expert의 복잡한 행동을 cost가 충분히 반영하도록 basis를 조절하는것이 어렵다는 확인하였습니다. 여기서 저자는 neural network 와 같이 좀 더 복잡한 표현이 가능한 모델을 가지고 approximation 해보자는 제안합니다.

5.1 Cost funciton & Jensen-Shannon divergence
이제 필요한 것은 basis function의 spanc으로 cost function이 제한되는 $\delta_{\mathcal{C}}$와 달리 cost function의 제한이 없는 cost regularizer입니다. 여기서 저자는 두 분포의 차이를 symmetirc하게 측정하는 metric인 Jenson-Shannon divergence를 제안합니다. 즉, 아래 14번 식에서 convex conjugate function $\psi^{*}$ 를 Jensen-Shannon divergence $D_{JS}$로 대체하도록하는 $\psi_{GA}$를 찾을 수 있으며,
$$
\underset{\pi}{\mathbf{minimize}},\psi_{GA}^{*}(\rho_{\pi}-\rho_{\pi_E})-\lambda H(\pi)=D_{JS}(\rho_{\pi},\rho_{\pi_E})-\lambda H(\pi)\qquad\qquad(15)
$$
이를 만족하는 cost regularizer $\psi_{GA}$는 다음과 같습니다.

여기서 conjugate function $\psi_{GA}^{*}$는 Jensen-Shannon divergence $D_{JS}$의 정의로부터 아래와 같이 정리할수 있습니다.
$$
\psi_{GA}^{*}(\rho_{\pi}-\rho_{\pi_E})=\underset{D\in(0,1)^{\mathcal{S}\times\mathcal{A}}}{\mathbf{sup}}\mathbb{E_{\pi}}[log{(D(s,a))}]-\mathbb{E_{\pi_E}}[log{(1-D(s,a))}]\qquad\qquad(14)
$$
이 식은 Generative adversarial network (GAN) 의 discriminator loss와 매우 유사합니다. (https://www.slideshare.net/HyungjooCho2/deep-generative-modelpdf 의 58page 참조)

다시말해 결국 저자는 section.4의 8번 식에서 사용한 smoothly penalizing regularizer $d_{\psi}(\rho_{\pi},\rho_E)\triangleq{\psi}^(\rho_{\pi},\rho_E)$ 를 GAN의 discriminator loss인 Jensen-Shannon divergence 형태로 의도적으로 유도하였으며, 결국 14번 식으로 부터 *RL-IRL 문제를 Generative adversarial network training problem으로 바꿀 수 있게됩니다. 저자는 이와같이 $\psi_{GA}$ 를 cost regularizer로 사용한 imitation learning을 "generative adversarial inmiation learning" 혹은 줄여서 "GAIL" 이라고 정의하였으며, 15번 식으로 부터 새롭게 정의한 아래 loss fuction의 Saddle point $(\pi, D)$를 GAIL을 사용함으로서 expert의 의도를 충분히 반영하면서도 large envrionment에서 사용가능한 policy를 학습합니다.
$$
\mathbb{E_{\pi}}[log{(D(s,a))}]-\mathbb{E_{\pi_E}}[log{(1-D(s,a))}]-\lambda H(\pi)\qquad\qquad(16)
$$
뿐만아니라 D(s,a)가 1에 가까우면 agent, 0에 가까우면 expert의 pair라고 구별하도록 discriminator를 학습합니다. GAIL이 기존의 APP와 다른 점은 IRL과 RL이 합쳐졌기 때문에, IRL에서 cost function을 업데이트 할때마다 매번 RL에서 optimal policy를 찾는 엄청난 비효율적인 연산 없이 IRL과 RL을 동시에 학습할 수 있다는 점입니다. 또한 기존의 최적화 문제를 풀었던 접근법과 달리 policy와 discrimiator 모두 neural network 를 사용하였기 때문에 parameter에 대한 gradient descent 만으로 학습이 가능해졌습니다.
하지만 여기서 RL은 policy gradient (PG) 부류 알고리즘으로 학습시키며, PG가 high variance와 small step required 문제를 가지고 있습니다. 이를 해결하고자 저자는 효율적으로 gradient를 업데이트 하는 Trust region policy optimization (TRPO) 알고리즘을 사용합니다.

지금까지의 내용을 알고리즘으로 표현하면 다음과 같습니다.

GAIL이 나온 시점에서는 TRPO가 SOTA알고리즘이었지만, 이후 유사한 성능에 보다 더 쉬운 PPO가 나왔으므로 대체가 가능해 보입니다.
6. Experiments
이제 GAIL의 성능을 검증하고자 MuJoCo의 9개의 pysics-based contol task에서 실험을 진행합니다. 또한 각 task마다 GAIL과의 성능 비교를 위한 baseline으로 다음 총 3개의 알고리즘을 사용합니다.
- Behavior cloning: supervised learning 방식으로 policy를 학습
- Feature expectation matching (FEM): $c(s,a)$를 basis function의 linear combination set에서 결정
- Game theoretic apprenticeship learning (GTAL): $c(s,a)$를 worst case excess cost 사용
결과는 다음과 같습니다.

Reacher룰 제외한 모든 MuJoCo 환경에서 GAIL은 적은 data set으로도 expert performance와 최소 70% 이상을 보여주며 다른 알고리즘보다 뛰어난 성능을 보여주었으며 적은 dataset에서도 한번에 충분히 expert와 유사해졌습니다. 이에 반해 다른 알고리즘의 경우 data set을 늘려도 expert에 도달하지 못했습니다. Reacher의 경우 적은 데이터에선 sample efficiency가 더 좋은 behavior cloning이 더 나은 성능을 나타내었습니다.
7. Discussion and Outlook
GAIL은 상당히 sample effient한 알고리즘이지만, TRPO의 학습을 위한 충분한 data의 양은 필요합니다. 저자는 sample efficiency가 높은 behavoior cloning으로 파라메터를 초기화할 경우 학습속도를 더 올릴 수 있을 것이라고 합니다. GAIL은 기본적으로 model free 방식입니다. 반면 Guided cost learning 알고리즘은 model-based 방식입니다. 두 알고리즘이 전혀 다르게 유도되었음에도 불구하고 GAIL과 Guided cost learning은 모두 policy optimization과 cost fitting (discriminator fitting)을 번갈아하는 특징을 같습니다. 학습중 expert와 상호작용이 가능한 DAgger와 같은 알고리즘과 달리, GAIL은 다른 IRL과 같이 학습중에는 expert와 상호작용을 할 수 없습니다. 저자는 궁긍적으로 environment model 선택과 expert interation을 잘 결합하는 알고리즘이 sample complexity 측면에서 앞서나갈 것이라고 내다보았습니다.
GitHub - reinforcement-learning-kr/lets-do-irl: Inverse RL algorithms (APP, MaxEnt, GAIL, VAIL)
Inverse RL algorithms (APP, MaxEnt, GAIL, VAIL). Contribute to reinforcement-learning-kr/lets-do-irl development by creating an account on GitHub.
github.com
'프로젝트 > GAIL 하자' 카테고리의 다른 글
| 7. Variational Discriminator Bottleneck (0) | 2023.02.21 |
|---|---|
| 5. Maximum Entropy Inverse Reinforcement Learning (1) | 2023.02.21 |
| 4. Maximum Margin Planning (0) | 2023.02.20 |
| 3. Apprenticeship Learning via Inverse Reinforcement Learning (0) | 2023.02.19 |
| 2. Algorithms for Inverse Reinforcement Learning (0) | 2023.02.19 |
