Author: 이승현
Date: February 1, 2019
Inverse RL 2번째 논문

- Author : Pieter Abbeel, Andrew Y. Ng
- Paper Link : http://people.eecs.berkeley.edu/~russell/classes/cs294/s11/readings/Abbeel+Ng:2004.pdf
- Proceeding : International Conference on Machine Learning (ICML) 2004
0. Abstract
reward가 주어지지 않은 Markov decision process 문제에서, 특히나 reward를 어떻게 줄지 하나하나 고려하는것이 힘들 때 전문가의 시연을 보고 학습하는것은 상당히 효과적인 접근입니다. 이러한 관점에서 이 논문은, 전문가가 선형 조합으로 표현한 reward function을 최대화 하려는 행동을 했다고 가정하고 이 reward function을 복구하고자 inverse reinforcement learning 을 사용하는 알고리즘을 제안합니다. 이와 함께 알고리즘이 작은 횟수로도 학습이 가능하며, 전문가 시연과 비슷한 성능을 얻을 수 있음을 실험을 통해 보이고자 합니다.
1. Introduction
어떤 task를 배울때 전문가의 시연(demonstration)을 보고 배우는것을 Apprenticeship learning 이라고 합니다. (혹은 learning by watching/ imitation learning/ learning from demonstration이라고도 불립니다.) Apprenticeship learning은 여러 접근 방법이 있는데, 대표적으로 '전문가의 행동을 그대로 따라하는 것'과 '행동의 의도를 학습하는것'입니다.
예를 들어 봅시다. 운전을 배울 때 전문가가 50번 국도의 300m 지점에서 핸들을 왼쪽으로 30도 돌리는 행동을 그대로 따라하기만 한다면, 동일 위치라도 갑자기 옆 차선의 운전자가 끼어드는것과 같은 임의의 상황에서 아무런 대응을 할 수 없습니다. 이렇게 연속적인 상황에서 정답인 행동을 보여주고 그대로 따라하도록 policy를 학습하는 방식을 Behavior cloning 이라고 하는데, 이는 경로가 길어질 수록 오차가 커지며 상태가 조금만 달라져도 잘 대응하지 못하는 단점이 있습니다. 즉, 모방(mimic) 문제에만 적용이 가능하며 supervized learning의 단점을 그대로 가지게 됩니다.
때문에 task에 대한 최적의 policy를 배우기 위해선 전문가의 행동을 그대로 따라하기보단 그 행동이 갖는 함축적인 의미(혹은 의도)를 학습하는것이 더 효과적이며, 이 논문 에서 다루는 알고리즘(이하 APP)은 이를 위해 reward function을 feature들의 선형조합으로 표현한 다음 이를 Inverse reinforcement learning 으로 학습하는 방법을 제안합니다.
추가적으로 APP는 버클리 BAIR 그룹의 Peter Abbeel 교수님께서 스탠포드시절 Andrew Ng 교수님과 쓰신 논문입니다. 당시 Abbeel 교수님은 강화학습 RC 헬기 연구를 하면서 manual reward의 한계 및 Reward shaping 의 필요성을 크게 느껴 APP 연구를 진행하셨습니다. 2004년 연구인 만큼 뉴럴넷보단 최적 설계 문제(Linear Progamming, Quadratic Programming; LP, QP)로 접근하였고, LP와 QP 로 reform시 스탠포드 최적화이론의 대가이신 Boyd 교수님의 접근법에 영향을 많이 받은것이 보입니다.
2. Preliminaries
알고리즘을 소개하기에 앞서 알고리즘에 사용 될 표기법 및 개념들을 몇 가지 짚고 넘어가겠습니다. (finite state) Markov Decision Process (MDP) 는 tuple $(S,A,T,\gamma,D,R)$로 표기합니다. 여기서 $S$는 finite set of states, $A$는 set of actions, $T={P_{sa}}$는 set of state transition probabilities, $\gamma \in [ 0, 1 ]$는 discount factor, $D$는 start state가 $s_{0}$인 initial-state distribution, 그리고 마지막으로 $R:S\mapsto A$는 크기가 1이하인 reward function 입니다. 이 논문은 전문가의 시연으로부터 reward function을 찾고자 하므로, reward가 없는 MDP인 $MDP \setminus R$를 다룹니다.
먼저 0에서 1사이의 요소를 갖는 vector of features인 $\phi : S\rightarrow [0,1]^k$을 가정합니다. 여기서 feature는 task를 수행할때 고려해야할 요소 정도로 볼 수 있는데, 예를 들어 자동차 주행 domain에서는 '몇 차선을 달리고 있는지', '앞 차와의 거리' 혹은 '다른 차와 충돌 여부' 등이 될 수 있습니다. 이와 같이 task에 대한 feature를 먼저 설계한 뒤, 전문가의 "true" reward function 을 $R(s)= \omega\cdot\phi(s)$ 와 같이 feature들의 선형조합이라고 가정하고, 구하고자 하는 reward의 크기를 1로 제한하고자 $||\omega^* ||_1\le 1$ 의 조건을 가정합니다. 결과적으로 (unkown) vector $\omega^{*}$는 task에 대한 각 고려 요소들의 상대적 weighting이라고 볼 수 있습니다. Policy $\pi$는 action에 대해서 states를 확률 분포와 mapping하는 역할을 합니다. 따라서 policy $\pi$의 value는 expectation으로 표현하며 다음과 같습니다.
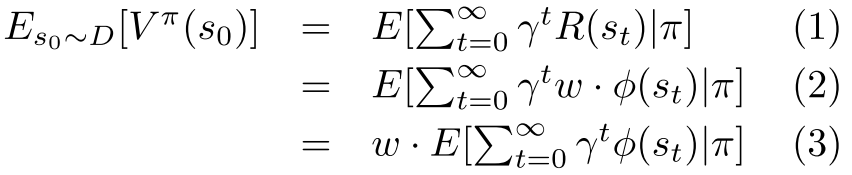
앞서 reward를 feature의 선형조합, 즉 weight vector와 feature vector의 곱으로 표현하고자 하였으므로, value는 (2)번 식과 같이 변형이 가능합니다. 이때 weight는 policy와 무관하므로 expectation 밖으로 빼내어 (3)번 식과 같이 나타내어 집니다. 여기서 weigth와 곱해진 expectation 항, 즉 expected discounted accumulated feature value vector를 아래와 같이 $\mu(\pi)$ 혹은 feature expection 라고 정의합니다.
$$
\mu(\pi)=E[\sum_{t=0}^{\infty}\gamma^t\phi(s_t)|\pi]\in\mathbb{R}^k
$$
이제 전문가가 보여준 시연(demonstration)에 대한 전문가의 policy를 $\pi_{E}$ 라고 가정하며, 이를 reward function $R^* =\omega^{^T}\phi$ 에 대한 optimal policy라고 간주합니다. 하지만 optimal policy가 직접적으로 주어지지는 않았으므로 이에 대한 expert's feature expectation $\mu_E=\mu(\pi_E)$를 구할 수 없으며, 대신 demonstration인 $m$개의 trajectory ${s_0^{(i)},s_1^{(i)},\dots\}_{i=1}^{m}$가 주어졌을 때, estimation of expert's feature expectation $\hat\mu_E$ 를 다음과 같이 추정이 가능합니다.
$$
\hat\mu_E=\frac{1}{m} \sum_{t=1}^{m}\sum_{t=0}^{\infty}\gamma^t\phi(s_t^{(i)})
$$
이후 APP에서 활용하는 inverse reinforce learning (IRL)에서는 $MDP \setminus R$를 풀고자 Reinforcement learning (RL) 을 사용하는데, 여기서는 RL 알고리즘의 종류 및 그 수렴성에 대한 구체적인 언급은 하지 않고 항상 optimal policy를 반환한다고 가정하겠습니다.
3. Algorithm
이 논문에서 다루고자 하는 문제는 $MDP \setminus R$과 feature mapping $\phi$, 그리고 전문가의 feature expectation $\mu_E$가 주어 졌을 때, $unkown$ reward function $R^* =\omega^{*^T}\phi$을 가진 전문가와 유사한 performance를 보이는 policy를 찾는 것입니다. 다시 말해 expert policy $\pi_E$와 learner policy $\tilde \pi$ 각각에 대한 value의 차이가 얼마나 작은지를 solution의 기준으로 하며 다음의 (6)번 식과 같이 쓸 수 있습니다.

앞서 2장에서 value는 weight와 feature expectation으로 표현가능하다고 정의하였으므로 (6)은 (7)과 같이 변형이 가능하며, $| x^Ty | \le || x ||_2 || y ||_2$의 성질에 따라 (8)과 같은 부등식이 성립합니다. 그리고 performance가 유사함의 기준을 충분히 작은 값 $\epsilon$ 으로 지정한다면 최종적으로 (9)의 부등식이 도출됩니다. 나아가 (8)과 (9)에서 앞서 언급한 조건 및 그 성질인 $||\omega ||_2\le || \omega || _1\le 1$을 고려한다면, 다루고자 하는 문제의 범위는 feature expectation $\mu(\tilde {\pi })$가 expert's feature expectation $\mu_E$과 가까워지게 하는 policy $\tilde {\pi }$를 찾는것 으로 좁혀집니다. 이 과정을 순차적인 알고리즘으로 나타내면 다음과 같습니다.

요약하자면 다음의 4 단계로 구성된 알고리즘이라고 볼 수 있습니다.
- Expert feature expectation과 feature expectation set로 부터 계산한 expert와 learner의 performance 차이를 t 로 정의하고, t를 최대화하는 weight를 찾는 과정. 다시말해 reward를 찾는 IRL step
- IRL step 에서 얻은 reward function에 대한 optimal policy를 찾는 RL step
- RL step에서 구한 policy로부터 Monte Carlo 시행을 통해 새로운 feature expectation을 구하고, 이를 feature expectation set에 추가
- a와 b의 IRL step $\Leftrightarrow$ RL step 반복하다 t가 𝜖 이하일 때, 즉 feature expectation이 충분히 가까워 졌을 때 학습 종료

위 step 1. 에서 t를 최대화 하는것은, learner에 비해서 expert의 performance를 더 잘 설명하는 reward function을 만들고자하는 것이며, 마치 틀린 시험문제에 대한 더 자세한 오답노트를 만드는것과 같습니다. 이렇게 expert와의 차이가 커야 learner가 RL step에서 이 reward function으로 policy를 다시 학습 했을때 더 발전을 하기 때문입니다. t를 최대화 하는 과정은 위 논문의 알고리즘에서 step 2에 해당합니다. 이는 Linear IRL(Ng & Russell, 2000) 에서 사용한 Linear programming (LP) 최적화 문제와 유사해 보이지만, $\omega$ 에 대한 2-norm (L2)이 constraint인 차이점이 있습니다. APP 논문을 작성할 당시엔 L2 norm constraint를 포함한 LP를 풀 수 있는 Convex optimization solver가 없었기 때문에, 저자는 논문에서 Quadratic programming (QP) 의 일종인 Support vector machine (SVM)을 사용하는 최적화 방법을 제안합니다.
아래 그림과 같이 expert feature expectation는 +1로, 학습 중인 learner feature expectation은 -1로 labelling 할 경우, step 2를 SVM 문제로 정의해서 풀수 있게됩니다. 그림은 이해를 돕기위해 feature가 두개만 있을 경우입니다.

즉, step 2에 대한 LP 형태인 아래 (10)~(12)의 식을, SVM의 형태인 (13)으로 변환할 수 있습니다.


이와같이 SVM으로 reform된 최적화 문제는 SVM이 QP의 일종이므로 일반적인 QP solver로도 쉽게 optimal weight $\omega$를 구할 수 있게됩니다.
LP, QP, SVM에 대한 내용은 다음 링크들에 자세히 소개되어 있으니 참고하시기 바랍니다.
- 모두를 위한 컨벡스 최적화 (LP) : https://wikidocs.net/17850
- 모두를 위한 컨벡스 최적화 (QP) : https://wikidocs.net/17852
- KAIST 문일철 교수님 강의 (SVM) : https://youtu.be/hK7vNvyCXWc
물론 학습한 policy들 $\pi^{(i)}$에 의해 learner feature expectations $\mu^{(i)}$가 쌓이면 expert feature expectation과 learner feature expectation이 linearly separable 하지 않아 infeasible한 경우가 발생할 수 있으며, 이 때 엔지니어가 policy를 직접 선택해야하는 문제가 생깁니다. 이를 피하고자, 아래 그림과 같이 저자는 $\pi^{(i)}$ 와 mixture weight $\lambda_i$ 로 covex combinatioin set을 만들어 그 안에서 $\mu_E$ 와의 거리가 최소가 되는 새로운 feature expectation 선택하는 방법을 사용합니다.

convex combination으로 새로운 $\mu$ 를 구하는 최적화 문제는 다음과 같이 쓸 수 있습니다.
$$
\min || \mu_E - \mu ||_2, s.t. \mu=\sum_i\lambda_i\mu^{(i)}, \lambda\ge 0, \sum_i\lambda_i=1
$$
3.1 A simpler algorithm
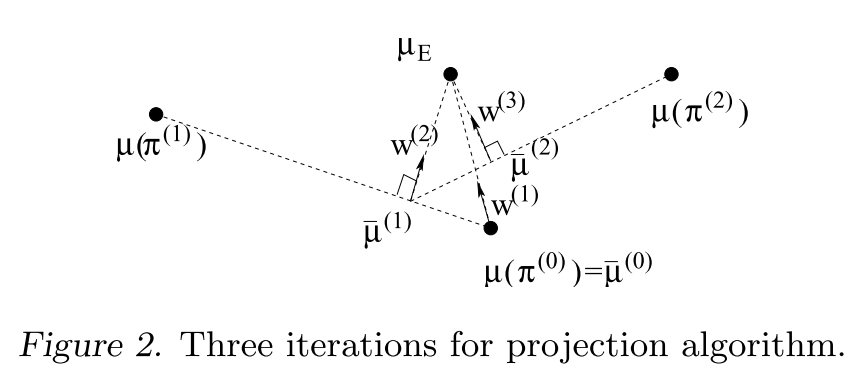
지끔까지 설명한 알고리즘은 QP (혹은 SVM) solver가 필요했으며, 이러한 QP기반의 알고리즘을 "max-margin" 방법이라고 합니다. 여기서 알고리즘을 조금 변형 하여 새롭게 구한 $\mu^{(i)}$ 를 차례차례 투영해가면서 $\mu_E$ 에 점차 가까워지도록 $\omega^{(i+1)}$ 를 구해나간다면 QP solver가 필요없는 최적화 접근이 가능하며 이를 "projection" 방법이라고 하겠습니다.
4. Experiments
이 논문은 앞서 설명한 알고리즘을 Gridworld와 Car driving simulation의 두가지의 환경에서 테스트 합니다. 각 실험에서 보여주고자 하는 바가 다르니 각각 자세히 살펴보도록 하겠습니다.
4.1 First experiment : grid world
첫번째 환경은 강화학습을 접해본 사람이라면 익숙한 Gridworld입니다. 128 x 128의 픽셀을 64개의 16 x 16 인 macro cell로 겹치지 않게 나누었는데, 그냥 일반적인 8 x 8 Gridworld라고 보면 됩니다.

4.1.1. Gridworld - 환경 설정
총 64개의 macro cell이 중 어느 macro cell에 위치해 있는지가 상태가 되며, agent는 각 macrocell에서 위, 아래, 좌, 우의 4가지 행동을 선택 할 수 있으나 30%의 확률로 선택과 다른 랜덤한 행동을 하게 됩니다. 그리고 APP 알고리즘의 성능을 가장 잘 확인하기 위한 목적으로 Gridworld가 sparse한 reward를 랜덤하게 갖는 환경을 가정합니다. 이 때 64개의 macrocell 에 대해서 현재 agent의 state $s$가 $i$번째 macrocell에 있는지의 유무를 하나의 feature $\phi_i(s)\quad i=1,...,64$로 보면 state별로 총 64개의 feature가 생깁니다.
또한 64개의 각 macrocell에 대해서 0.9의 확률로 zero reward $w_i^*=0$ 를, 0.1의 확률로 0에서 1사이에서 uniform 하게 샘플링한 non-zero reward $w_i^* \in [ 0, 1 ]$를 줍니다. 그리고 나서, 알고리즘의 'true' reward에 대한 가정에 따라 $w^*$ 의 1-norm은 1이되도록 non-zero reward를 normalize 합니다. 이와 같이 true Reward를 설정한 다음엔, experts의 optimal policy에 따른 trajectory를 수집합니다. 논문에서는 실험을 위해 약 100,000 개의 sampled trajectory를 준비하였고, Monte-Carlo estimation을 사용해 expert의 expectation performance를 계산했습니다.
4.1.2. Gridworld - 알고리즘 성능 비교
이제 설정된 Gridword환경과 계산된 expert performance로 APP알고리즘의 성능을 검증할 두가지 실험을 하는데, 실험에 앞서 Apprenticeship 알고리즘의 목적이 reward를 recover하지 않고 expert와 유사한 performance를 내는 것이므로 비교대상인 알고리즘들에 true reward는 알려주지 않는것을 전제로 합니다.
실험 1. QP vs Non-QP
Gridworld의 첫번째 실험은 앞서 3절에서 이야기한 APP 알고리즘의 두가지 버전인 QP 방식의 Max-margin 방법과 non-QP 방식의 projection 방법에 대한 비교입니다.

두 가지 버전 모두 30회의 iteration을 각 40번씩 반복 진행했고, 각 iteration에서 expert feature expectation과의 Euclidean distance 평균을 구한 그래프는 위와 같습니다. 두 가지 알고리즘 모두 꽤 유사한 수렴 속도를 보여주고 있으나 non-QP방식의 projection 알고리즘이 근소하게 더 뛰어납니다. projection 방법이 max margin 방법보다 근소하게나마 빠르게 수렴하는것은 QP의 hard margin에 의한 문제를 겪지 않고 바로 expert feature expectation으로 접근하기 때문이라고 생각됩니다.
실험 2. QP vs Non-QP
Gridworld의 두번째 실험은 APP알고리즘과 다른 3가지 알고리즘들의 sampling efficiency를 비교합니다. 이 때 APP도 아래와 같이 두가지 버전으로 나누는데, 즉, 좀 더 True reward의 구조에 가까운 reward function을 사용하게 했을때의 성능을 비교하고자 했다고 볼 수있습니다.
- Apprenticeship 1: non-zero weight feature를 알고리즘에 알려준 경우
- Apprenticeship 2: 모든 feature를 다 사용한 경우
비교대상이 되는 다른 3가지 알고리즘은 다음과 같습니다.
- Parameterized policy stochastic:
각 macrocell 에서 experts가 한 action별 empirical frequency에 따라 stochastic policy를 만들어 사용하는 알고리즘 - parameterized policy majority vote:
각 macrocell에서 observed된 가장 빈번한 action을 deterministic 하게 선택하는 알고리즘 - Mimic the expert:
expert가 지나간 state에서는 expert와 같은 action을 하고, expert가 지나가지 않은 state에서는 랜덤하게 action을 선택하는 알고리즘

비교 결과는 위 그래프와 같습니다. 위에서 부터 간략화된 feature를 사용한 IRL(초록), 모든 feature를 사용한 IRL(사이안), parameterized policy stochastic(분홍), parameterized policy majority vote(빨강), mimic the expert(파랑) 입니다. 확실히 APP 알고리즘이 다른 알고리즘들에 비해서 적은 sample 만으로도 expert에 가까운 성능을 보여줌을 확인할 수 있습니다. 더욱이 x축 스케일이 log인걸 감안하면 sampling efficiency의 차이는 매우 매우 큽니다.
좀 더 분석을 해보면, mimic the expert 알고리즘은 비효율 적이지만 expert performance에 도달한데 반해 두 가지 parameterized 방식 은 도달하지 못했습니다. 이는 알고리즘이 만들어낼 수 있는 policy의 다양성 때문인데, 실제로 가장 빈번했던 action 한가지만 deterministic하게 사용한 방식이 가장 낮은 성능을 보여주었고, stochastic한 방식은 조금 더 낫지만 여전히 expert가 보여준 action에 한정되어 있다는 한계로 제한된 성능을 보여주었습니다. 이에 반해 mimic the expert는 랜덤 선택을 넣음으로서 나머지 두 알고리즘에 비해 policy의 다양성이 더 증가 되어 expert performance에 도달 할 수 있었습니다.
IRL방식(여기서는 APP) 역시 두가지 방식에서 초기의 근소한 수렴속도 차이를 보여주는데, 이는 non-zero weight feature를 알고 있음으로서, 알고리즘의 Reinforcement learning 단계에서 좀더 true reward에 가까운 reward 로 policy estimation이 시작부터 가능했기 때문으로 보입니다.
4.2 Second experiment : Car driving simulation
두번째 실험에서는 expert의 다른 style에 대해서 알고리즘이 각각의 style을 동일하게 잘 모방 할 수 있는지를 car driving simulation을 통해 확인하고자 합니다.
4.2.1. Car driving - 환경 설정

Gridworld와 마찬가지로 환경에 대한 설명부터 하겠습니다. 주변의 빨간색 자동차들보다 빠른 25 m/s의 고정된 속도로 움직이는 파란색 자동차를 좌우로 움직일 수 있습니다. 선택할 수 있는 action은 총 5가지로, 왼쪽/중앙/오른쪽 레인으로 자동차를 이동시키는 action 3가지와 왼쪽/오른쪽의 초록색 비포장도로로 자동차를 이동시키는 2가지입니다. 알고리즘은 expert가 각 driving style에 따라 2분동안 보여주는 시연 정보를 사용하는데, 시뮬레이션은 10Hz의 속도로 샘플링을 하므로 총 1200 sample을 가진 trajectory를 수집했습니다. Gridworld때와 마찬가지로 expert와 알고리즘의 performance를 계산하기위해서 feature를 정하는데, 실험에서는 현재 자동차가 비포장로 및 레인의 5가지 위치 중 어디에 있는지의 5개의 feature $\phi_i$와, 현재 레인에서 가까운 차와의 거리를 -7 부터 +2까지로 1씩 discrete하게 나눈것의 10개의 feature $\phi_i$를 합쳐 총 15개의 feature를 설정하였습니다.
4.2.2. Car driving - 알고리즘 성능 검증
APP알고리즘이 모방하게 하고자 하는 expert의 driving style은 다음의 5가지입니다.
- Nice:
충돌을 피하는것을 최우선적으로 함. 또한 레인의 선호도 차이가 있음.
(오른쪽 > 중앙 > 왼쪽 > 비포장도로). - Nasty:
가능한 많은 충돌을 일으킴. - Right lane nice:
오른쪽 레인으로 달리되 충돌을 피하기 위해 오른쪽 비포장 도로를 사용함. - Right lane nasty:
오른쪽 비포장 도로를 달리되 충돌하기위해 오른쪽 레인으로 들어옴. - Middle lane:
충돌에 상관없이 중앙으로만 달림.
이 5가지 각 style 시연들을 딥러닝에서 흔히 하는대로 CNN에 2분짜리 비디오 화면을 넣는게 아니라는걸 주의바랍니다. 단지 위에서 말한 feature에 따라 계산한 performance 값을 주는 것을 의미합니다. 각각 30번의 iteration을 한 뒤의 학습 결과는 다음과 같습니다.
| Nice | Right lane nice | Middle lane |
 |
 |
 |
| Nasty | Right lane nasty | |
 |
 |
보다시피 결과가 상당히 좋습니다.
특히 주목할 점은 행동 그 자체를 따라하는것이 아니라 매 순간의 driving style을 잘 모방 하고 있다는 것입니다. 좀 더 수치적으로 성능을 분석해 보겠습니다. expert는 단지 시연을 한 것 뿐이지 일일히 보상을 주는 등의 true reward function을 따로 정하지 않았기 때문에 agent가 얼만큼의 보상을 받았는지로는 알고리즘의 성능을 판단할 수 없습니다. 대신 driving style을 얼마나 잘 모방했는지의 성능을 분석하는것은 feature expectation의 비교로 가능합니다. 5가지 style에 따라 순서대로 expert와 알고리즘의 결과를 정리한 아래의 표를 보겠습니다.

앞서 설명한 대로 실제 설정한 feature는 총 15가지 지만 설명의 간결함을 위해 여기서는 6가지 feature (Collision, Offroad Lest, LeftLane, MiddleLane, RightLane, Offroad Right) 만을 비교했습니다. 표에서 각 행은 1~5번의 style에 각각 해당하고, sytle 마다 expert의 feature expectation $\hat \mu_E$과 agent의 feature expection $\mu \left( \tilde { \pi } \right)$그리고 그에 따른 feature weight $\tilde { w }$ 가 정리되어있습니다.
expert와 agent의 feature expectation 모두 각각의 driving style의 특성에 잘 맞는 (interesting) feature가 더 큰 값을 가진다는걸 확인가능하며, expert와 agent의 feature expectation의 분포 또한 유사한것을 확인 할 수 있습니다. 더 나아가서, 알고리즘에 의해 최적화된 feature weight $\tilde { w }$를 보면 어떻게 동영상과 같은 agent의 policy가 나타나는지가 어느정도 직관적으로 이해가 됩니다. 예를들어 첫번째 Nice driving style의 경우 충돌과 비포장 feature에 대해선 음의 보상을 주고 있으며 오른쪽 레인에 대해선 다른 레인에 비해 더 큰 양의 보상이 생성되었습니다. 이는 위 driving style에서 설명한 아래의 의도를 충분히 반영하고 있다는것을 알 수 있습니다.
Nice: 충돌을 피하는것을 최우선적으로 함. 또한 레인의 선호도 차이가 있음.
(오른쪽 > 중앙 > 왼쪽 > 비포장도로).
5. Conclusions and Future work
이 논문은, 전문가가 선형 조합으로 표현한 reward function을 최대화 하려는 행동을 했다고 가정하고 이 reward function을 복구하고자 inverse reinforcement learning 을 사용하는 알고리즘을 제안하였습니다. 결과적으로 실험을 통해 제시한 알고리즘이 작은 횟수로도 학습이 가능하며, 전문가 시연과 비슷하거나 더 나은 성능을 얻을 수도 있음을 확인하였습니다. 하지만 demonstration을 설명할 feature 수가 많아지면 reward function이 fearture들의 선형조합으로 나타낼 수 있다는 초기 가정을 보장할 수 없게됩니다. feature들에 대해서 비선형으로 reward를 나타내거나 자동으로 feature를 설계하거나 선택하는것은 매우 중요하며, 이에 대한 연구가 많이 필요합니다.
GitHub - reinforcement-learning-kr/lets-do-irl: Inverse RL algorithms (APP, MaxEnt, GAIL, VAIL)
Inverse RL algorithms (APP, MaxEnt, GAIL, VAIL). Contribute to reinforcement-learning-kr/lets-do-irl development by creating an account on GitHub.
github.com
'프로젝트 > GAIL 하자' 카테고리의 다른 글
| 6. Generative Adversarial Imitation Learning (0) | 2023.02.21 |
|---|---|
| 5. Maximum Entropy Inverse Reinforcement Learning (1) | 2023.02.21 |
| 4. Maximum Margin Planning (0) | 2023.02.20 |
| 2. Algorithms for Inverse Reinforcement Learning (0) | 2023.02.19 |
| 1. Let's do Inverse RL Guide (1) | 2023.02.18 |
