Author: 이동민
Date: January 28, 2019
Inverse RL 1번째 논문

- Author : Andrew Y. Ng, Stuart Russell
- Paper Link : http://ai.stanford.edu/~ang/papers/icml00-irl.pdf
- Proceeding : International Conference on Machine Learning (ICML) 2000
0. Abstract
이 논문은 Markov Decision Processes에서의 Inverse Reinforcement Learning(IRL)을 다룹니다. 여기서 IRL이란, observed, optimal behavior이 주어질 때 reward function을 찾는 것입니다.
IRL은 두 가지 장점이 존재합니다.
- 숙련된 행동을 얻기 위한 apprenticeship Learning
- 최적화된 reward function을 알아내는 것
이 논문에서는 IRL의 reward function에 대해 세 가지 알고리즘을 제시합니다.
- 첫 번째와 두 번째는 전체의 policy를 알고 있는 case를 다루는 것입니다. finite state space에서의 tabulated reward function과 potentially infinite state space에 대한 reward function의 linear functional approximation을 다룹니다.
- 세 번째로는 observed trajectories의 finite set을 통해서만 policy를 알고 있을 때 더 다양한 realistic case에 대한 알고리즘입니다.
이 논문은 2000년에 나온 논문으로서 그 당시에 어떻게 하면 reward function을 역으로 찾을 수 있는지를 증명을 통해서 다루고 있고, 왜 reward function이 중요한 지를 중요하게 말하고 있습니다. 그러니까 IRL을 통해 reward를 얻어 RL을 하는 실질적인 학습을 말하는 논문보다는 reward function에 대해서 말하고 있고 이에 따른 알고리즘들을 말하는 논문입니다. "reward function은 이렇게 생겨야 돼! 그리고 우리는 이러한 알고리즘들을 통해 reward function을 찾아낼 수 있어!"라는 듯이 말하고 있습니다.
위에서 말한 세 가지 알고리즘의 중요한 문제는 degeneracy입니다. 여기서 degeneracy란, 어느 observed policy가 optimal한 지에 대하여 reward function의 large set이 존재하는지에 관한 degeneracy를 말합니다. 다시 말해 이러한 reward function의 large set을 찾기 위한 알고리즘이 존재하는지, degeneracy는 없는 지를 말하는 것입니다. 이 논문에서는 degeneracy를 없애기 위해서 natural heuristics를 제시합니다. 그리고 natural heuristics를 통해 IRL에 대해서 효과적으로 해결가능한 linear programming formulation을 나타냅니다.
추가적으로 이러한 문제를 하나의 용어로 말하면 "ill-posed problem" 이라고 합니다. ill-posed problem을 검색하면 위키피디아에 있는 well-posed problem이 먼저 나오는데 여기서 말하는 well-posed problem이란 특정한 solution이 존재하고, 그 solution이 unique 하다고 나와있습니다. 반대로, 역강화학습에서는 reward가 정해진 것이 아니라 여러 가지 형태의 값으로 나타날 수 있기 때문에(정해진 값이 아니기 때문에, not unique) ill-posed problem이라고 볼 수 있습니다.
실험에서는 이 논문에서의 알고리즘들을 통해 간단한 discrete/finite and continuous/infinite state problem들을 해결합니다.
1. Introduction
IRL은 Russell이 쓴 논문에서 비공식적으로 정의합니다.
Given :
- 시간에 따른 agent의 행동들
- 필요하다면, agent의 sensory input들
- 가능하다면, 환경의 모델 이 주어질 때
Determine : reward function을 최적화하는 것
뒤이어 나오는 두 가지 언급을 통해서 IRL이 왜 중요한 지를 알아봅시다.
첫 번째로 animal and human learning에 대한 computational model로서 RL의 잠재적인 사용입니다. 예를 들어 벌이 먹이를 찾는 모델이 있다고 했을 때 여러 꽃들 사이에서의 reward가 꿀에 대한 간단한 saturating function이라고 가정해봅시다. reward function은 보통 고정되어 있고 + 우리가 정하고 + 이미 알고 있습니다. 하지만 animal and human behavior을 조사할 때 우리는 추가적으로 알지 못하는 reward function까지도 생각해야 합니다. 다시 말해 reward function의 multiattribute(다속성)도 생각을 해야 한다는 것입니다. 벌이 바람과 벌을 먹이로 하는 포식자들로부터 비행 거리, 시간, 위험 요소들을 고려하여 꿀 섭취를 할 수도 있습니다. 사람의 경제적 행동 속에서도 이러한 경우가 많습니다. 따라서 IRL은 이론적으로 생물학, 경제학, 또는 다른 분야들까지 포함하는 근본적인 문제에서 나타낼 수 있습니다.
두 번째로는 특정한 도메인에서 잘 행동할 수 있는 intelligent agent를 구성할 수 있다는 것입니다. 보통 agent designer들은 그들이 정하는 reward function의 optimization이 "desirable" 행동을 만들 것이라는 굉장히 rough한 생각을 가질 수 있습니다. 그렇지만 아주 간단한 RL 문제라도 이것은 agent designer들을 괴롭힐 수 있습니다. 여기서 한 가지 사용할 수 있는 것이 바로 다른 "expert" agent의 행동입니다.
가장 넓은 set인 "Imitation Learning" 안에는 일반적으로 expert agent를 통한 학습이 두 가지 방법이 있습니다.
- 첫 번째로는 "IRL" 이라는 것이 있고, IRL을 이용한 하나의 방법으로서 Pieter Abbeel이 주로 쓰는 알고리즘의 이름인 Apprenticeship Learning이라는 것이 존재합니다. 그래서 IRL이란 teacher의 demonstation에서의 optimal policy를 통해 reward를 찾는 것을 말합니다.
- 다음으로 "Behavioral Cloning"이라는 것이 있습니다. 아예 supervised learning처럼 행동을 복제한다고 생각하면 됩니다.
일반적으로 IRL을 통해서 cost를 얻고, RL을 통해서 policy를 찾는 것이 모든 IRL의 목적입니다. 하지만 이렇게 2 step을 해야 한다는 점에서 많은 complexity가 생기고, 그렇다고 IRL을 통해서 얻은 cost만 가지고는 별로 할 수 있는 게 없습니다. 따라서 앞서 말한 과정을 2 step만에 하는 것이 아니라 1 step만에 풀어버리는 논문이 바로 Generative Adversarial Imitation Learning(GAIL)이라는 논문입니다. 이후의 논문들은 다 GAIL을 응용한 것이기 때문에 GAIL만 이해하면 그 뒤로는 필요할 때 찾아서 보면 될 것 같고, GAIL이라는 것을 이용하여 여러 가지 연구를 해볼 수도 있을 것 같습니다.
이 논문에 나오는 section들은 다음과 같습니다.
- Section 2 : finite Markov Decision Processes(MDPs)의 formal definition들과 IRL의 문제를 다룹니다.
- Section 3 : finite state spaces에서 주어진 policy 중의 어느 policy가 optimal한 지에 대해 모든 reward function의 set을 다룹니다.
- Section 4 : reward function의 explicit, tabular representation이 가능하지 않을 수 있기 때문에 large or infinite state spaces의 case를 다룹니다.
- Section 5 : observed trajectories의 finite set을 통해서만 policy를 안다고 했을 때, 더 realistic case에 대해서 다룹니다.
- Section 6 : 앞서 언급했던 세 가지 알고리즘을 적용하여 discrete and continuous stochastic navigation problems와 mountain-car problem에 대한 실험부분이 나옵니다.
- Section 7 : 결론과 더 나아가 연구되어야할 방향에 대해서 다룹니다.
2. Notation and Problem Formulation
먼저 IRL version의 notation, definitions, basic theorems for Markov decision processes(MDPs)에 대해서 알아봅시다.
2.1 Markov Decision Processes
A finite MDP is a tuple $(S, A, {P_{sa}}, \gamma, R)$
- $S$ is a finite set on $N$ states.
- $A = {a_1, ... , a_k}$ is a set of $k$ actions.
- $P_{sa} (\cdot)$ are the state transition probabilities upon taking action $a$ in state $s$.
- $\gamma \in [0,1)$ is the discount factor.
- $R : S \rightarrow \mathbb{R}$ is the reinforcement function (reward function) bounded absolute value by $R_{max}$.
$R$에 대해 간단하게 말하기 위해서 $R(s,a)$보다 $R(s)$로서 reward $R$을 정의했습니다. $R$같은 경우, 사실 정의하기 나름인 것 같습니다. 이 논문에서는 $R(s, a)$로 생각하는 것보다 $R(s)$로 생각하는 것이 편하고 간단하기 때문에 이렇게 notation을 적은 것 같습니다. 아무래도 역강화학습에서 action $a$까지 생각해 주면 추가적인 notation이 더 나오기 때문에 복잡해집니다. 또한 사실 우리가 최적의 행동만 안다면 보상을 행동까지 생각해 줄 필요는 없기 때문에 $R(s)$라고 적었다고 봐도 될 것 같습니다. 역강화학습 논문들이 다 $R(s)$을 사용하는 것은 아닙니다. 논문마다 case by case로 쓸 수 있는 것 같습니다.
- Policy is defined as any map $\pi : S \rightarrow A$.
- Value function evaluated at any state $s_1$ for a policy $\pi$ is given by
$$ V^\pi (s_1) = \mathbb{E} [R(s_1) + \gamma R(s_2) + \gamma^2 R(s_3) + \cdots | \pi] $$
- Q-function is여기서 notation $s' \sim P$는 $s'$를 $P_{sa}$에 따라 sampling 한 것입니다.
- $ Q^\pi (s, a) = R(s) + \gamma \mathbb{E}_{s' \sim P} [V^\pi (s')] $
- Optimal value function is $V^* (s) = sup_\pi V^\pi (s)$. (sup is supremum, 상한, 최소 상계)
- Optimal Q-function is $Q^* (s,a)(s, a) = sup_\pi Q^\pi (s, a)$.
위의 모든 function들은 discrete, finite spaces에서 정의합니다.
마지막으로 Symbol $\prec$ and $\preceq$ denote strict and non-strict vectorial inequality - i.e., $x , \prec , y$ if and only if $, \forall i , , x_i < y_i$
2.2 Basic Properties of MDPs
IRL 문제의 solution에 대해 MDPs와 관련된 두 가지 classical result가 필요합니다.
Theorem 1 (Bellman Equations) : MDP $M = (S, A, {P_{sa}}, \gamma, R)$ and policy $\pi : S \rightarrow A$가 주어질 때, 모든 $s \in S$, $a \in A$에 대해서 $V^\pi$ 와 $Q^\pi$는 다음을 만족합니다.
$$\begin{equation}
V^\pi(s)=R(s)+\gamma \sum_{s^{\prime}} P_{s \pi(s)}\left(s^{\prime}\right) V^\pi\left(s^{\prime}\right)
\end{equation}$$
$$\begin{equation} Q^\pi (s, a) = R(s) + \gamma \sum_{s'} P_{sa} (s') , V^\pi (s') \end{equation}$$
Theorem 2 (Bellman Optimality) : MDP $M = (S, A, {P_{sa}}, \gamma, R)$ and policy $\pi : S \rightarrow A$가 주어질 때, $\pi$는 $M$에 대해 optimal policy라는 것은 $\equiv$ 모든 $s \in S$에 대해 다음과 수식과 같습니다.
$$\begin{equation} \pi (s) \in arg\max_{a \in A} Q^\pi (s,a) \end{equation}$$
Theorem 1, 2의 증명은 서튼책에 있고, 여기서는 추가적으로 다루지 않겠습니다.
2.3 Inverse Reinforcement Learning
IRL의 문제는 observed 행동을 설명할 수 있는 reward function을 찾는 것입니다. 그래서 가장 먼저 무엇을 하고 싶은 것이냐면, state space가 finite이고, model은 이미 알고 있고, complete policy가 observe 된 simple case부터 시작하고자 합니다. 다시 말해 $\pi$가 optimal policy일 때, 가능한 한 reward function의 set을 찾고자 하는 것입니다. 추가적으로 action들을 renaming 함으로써 $\pi (s) \equiv a_1$ (여기서 $a_1$는 임의의 하나의 행동)라는 것을 가정할 것입니다. 이 trick은 notation을 단순화하기 위해 사용될 것입니다.
3. IRL in Finite State Spaces
이번 section에서는 주어진 policy 중의 어느 policy가 optimal 한 지에 대해서 모든 reward functions의 set에 대한 간단한 정의를 할 것입니다. 그리고 모든 reward functions의 set에 degeneracy를 없애기 위해서 간단한 heuristic 방법인 "Linear Programming" (Wikipedia, 위키백과)을 제안합니다.
Linear Programming에 대해서 간략하게만 알아봅시다. 대부분의 사람들은 Linear Programming(선형 계획법) 보다 더 친숙한 Dynamic Programming(동적 계획법)을 알고 있는 경우가 많습니다. 여기서 "Dynamic"이란 동적, 즉 시간에 따라 변하며 다단계적인 특성을 말합니다. 그리고 "Programming"이란 컴퓨터 프로그래밍이 아니라 무언가를 계획하여 최적의 program을 찾는 방법을 말합니다. 한마디로 "시간에 따라서 큰 문제들 안에 작은 문제들이 중첩된 경우에 전체 큰 문제를 작은 문제로 쪼개서 최적의(optimal) program을 찾는 방법으로 풀겠다"라는 것입니다.
이와 비슷하게 Linear Programming, 선형 계획법도 Programming(계획법)이 들어갑니다. 그러니까 선형 계획법 또한 무언가를 계획하는 것으로서 "최적의 program을 찾는 방법으로 풀겠다."라는 것인데, 앞에 Linear만 추가적으로 붙었습니다. 정리하자면, "최적화 문제 일종으로 주어진 선형 조건들을 만족시키면서 선형인 목적 함수를 최적화하여 풀겠다."라는 것입니다. 이 Linear Programming(LP)은 주로 Operations Research(OR)에서 가장 일반적인 기법으로 뽑힙니다.
관련하여 예를 한번 들어보겠습니다. 아래의 예는 위키백과에 있는 예입니다. 홍길동 씨가 두 가지 종류의 빵을 판매하는데, 초코빵을 만들기 위해서는 밀가루 100g과 초콜릿 10g이 필요하고, 밀빵을 만들기 위해서는 밀가루 50g이 필요합니다. 재료비를 제하고 초코빵을 팔면 100원이 남고, 밀빵을 팔면 40원이 남습니다. 오늘 홍길동 씨는 밀가루 3000g과 초콜릿 100g을 재료로 갖고 있습니다. 만든 빵을 전부 팔 수 있고 더 이상 재료 공급을 받지 않는다고 가정한다면, 홍길동 씨는 이익을 극대화하기 위해서 어떤 종류의 빵을 얼마나 만들어야 할까요? 선형 계획법을 통해서 알아봅니다!
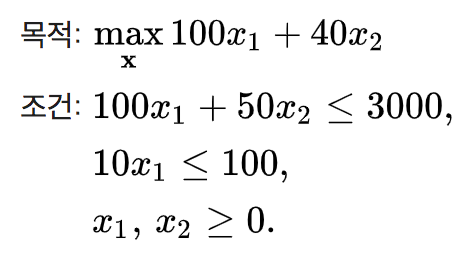
여기서 $x_1$은 초코빵을 $x_2$는 밀빵의 개수를 의미하는 변수입니다. 그림으로 나타내면 아래와 같이 가장 많은 이익을 남기는 방법은 초코빵 10개와 밀빵 40개를 만드는 것이고, 그렇게 해서 얻을 수 있는 최대 이익은 2600원입니다.
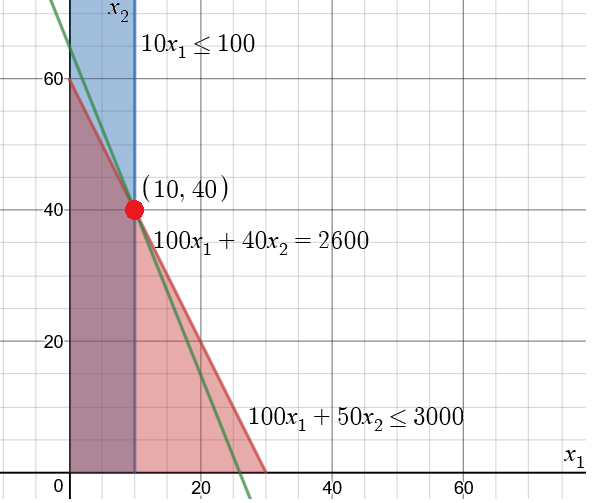
이익이 최대가 될 때는 이익을 나타내는 직선이 해가 존재할 수 있는 영역 중 원점에서 가장 떨어진 점 (10, 40)에 접할 때입니다. $100 x_1 + 40 x_2 = 2600$
3.1 Characterization of the Solution Set
Theorem 3 : Let a finite state space $S$, a set of actions $A = {a_1, ... , a_k}$, transition probability matrices ${P_a}$, a discount factor $\gamma \in (0, 1)$이 주어질 때, $\pi (s) \equiv a_1$에 의해 주어진 policy $\pi$가 optimal인 것은 $\equiv$ 모든 $a = a_2, ... , a_k$에 대해서 reward $R$이 아래의 수식을 만족하는 것과 같습니다.
$$\begin{equation}
(P_{a_1} - P_a)(I - \gamma P_{a_1})^{-1} R \succeq 0
\end{equation}$$
Proof. $\pi (s) \equiv a_1$로 인하여, Equation (1)은 $V^\pi = R + \gamma P_{a_1} V^\pi$이라고 쓸 수 있다. 따라서 아래의 수식으로 쓸 수 있습니다.
$$
V^\pi = (I - \gamma P_{a_1})^{-1} R
$$
위의 수식에서 주석처리가 되어있는 것을 보니 저자가 할 말이 더 있는 것 같습니다. $I - \gamma P_{a_1}$(여기서 $I$는 단위행렬)은 항상 invertible(역으로 되는)합니다. 실제로 정말 invertible 한 지를 보기 위해 transition matrix인 $P_{a_1}$가 복잡한 공간에 unit circle(단위원)에서 모든 eigenvalue들을 가진다는 것을 먼저 언급합니다. 다시 말해 $\gamma < 1$일 때, matrix $\gamma P_{a_1}$가 unit circle 내에 모든 eigenvalues를 가진다는 것을 말합니다. (특히 여기서 1은 eigenvalue가 될 수 없습니다.) transition matrix의 특성상 이렇게 되는 것이기 때문에 기억하는 것이 좋습니다. 뒤이어 위의 특성은 $I - \gamma P_{a_1}$이 zero eigenvalue를 가지고 있지 않고, ($\gamma$ 때문에 $I - \gamma P_{a_1}$가 0~1 사이에 있게 됩니다.) 이것과 동치로 말할 수 있는 것이 singular가 아니라는 것을 의미합니다. 참고로 singular 하다는 것은 해당되는 행렬이 역행렬이 존재하지 않는다는 것을 말합니다.
정리하자면, $I - \gamma P_{a_1}$ → zero eigenvalue가 없다. $\equiv$ sigular 하지 않다. $\equiv$ 역행렬이 존재한다.
추가적인 자료
- Stationary distribution relation to eigenvectors and samplices in Markov chain
- 특이값 분해(Singular Value Decomposition, SVD)의 활용)
다시 Proof를 따라가 봅니다. Equation (2)를 (3)으로 대체하면, $\pi \equiv a_1$가 optimal 하는 것은 $\equiv$ 아래의 수식과 같습니다.
$$
a_1 \equiv \pi (s) \in arg\max_{a \in A} \sum_{s'} P_{sa} (s') V^\pi (s') \forall s \in S
$$
$$
\Leftrightarrow \sum_{s'} P_{sa_1} (s') V^\pi (s') \geq \sum_{s'} P_{sa} (s') V^\pi (s') \forall s \in S, a \in A
$$
$$
\Leftrightarrow P_{a_1} V^\pi \succeq P_a V^\pi \forall a \in A \setminus a_1
$$
$$
\Leftrightarrow P_{a_1} (I - \gamma P_{a_1})^{-1} R \succeq P_a (I - \gamma P_{a_1})^{-1} R \forall a \in A \setminus a_1
$$
여기서 $a \in A \setminus a_1$이란 $a_1$을 제외한 set of actions $A$에 있는 $a$들을 말한다.
Remark. 매우 비슷한 argument를 사용하여 추가적인 언급을 합니다. $(P_{a_1} - P_a)(I - \gamma P_{a_1})^{-1} R \succ 0$라는 조건이 $\pi \equiv a_1$가 unique optimal policy가 되는 것에 필요하고, 충분하다고 볼 수 있습니다. (또한 추가적으로 위에 증명에 모든 inequalities를 strict inequalities로 대체함으로써) finite-state MDPs에 대해, 이러한 결과는 IRL의 solution인 모든 reward function들의 set을 정의합니다. 그러나 여기에는 두 가지 문제점이 있습니다.
- $R = 0$ (and indeed any other constant vector)은 항상 solution입니다. 다시 말해 만약 우리가 어떠한 행동을 취했을지라도 reward가 항상 같다면, $\pi \equiv a_1$을 포함하여 어떠한 policy들은 항상 optimal 하다는 것입니다. $\pi$가 unique optimal policy라는 점에서는 이 문제를 완화시키지만, 전체적으로 만족시키진 않습니다. 왜냐하면 보통 0에 임의적으로 가까운 일부 reward vector들이 여전히 solution이 될 수 있기 때문입니다.
- 대부분의 MDPs에서, criteria (4)를 만족시키는 R에 대한 많은 choice들이 있습니다.
그렇다면 우리는 어떻게 많은 reward function들 중의 하나를 결정할 수 있을까요?
다음 section을 통해서 이러한 문제점들을 해결할 수 있는 natural criteria를 알아봅시다!
3.2 LP Formulation and Penalty Terms
위의 질문에 대한 답변으로 명확하게 말하자면, Linear Programming(LP)은 Equation (4)로 인한 문제점들에 대해 실행 가능한 point로서 사용될 수 있습니다. 그래서 R을 고를 수 있는 한 가지 natural 한 방법은 가장 먼저 $\pi$를 optimal 하도록 만드는 것입니다. 또한 $\pi$로부터 어떠한 single-step deviation(편차)을 가능한 한 costly 하게 만드는 것입니다. 쉽게 말해 최적의 행동이 있다면 최적의 정책을 찾을 수 있고, 최적의 정책을 찾을 수 있다면 R을 고를 수 있다는 것입니다.
수식으로 표현해 보면, (4)를 만족시키는 모든 function R 중에서, 다음의 수식을 maximize 하도록 하는 $a_1$을 고를 수 있습니다.
$$\begin{equation} \sum_{s \in S} (Q^\pi (s, a_1) - \max_{a \in A \setminus a_1} Q^\pi (s, a)) \tag{6} \end{equation}$$
수식을 설명해 보면 quality of the optimal action과 quality of the next-best action 사이의 differences의 sum을 maximize 하는 것을 말합니다.
추가적으로 다른 모든 Q값들이 동등할 때, 대부분의 small rewards에 대한 solution은 "simpler"하도록 optional 하게 objective function이 $-\lambda ||R||_1$ ($\ell_1$-penalty)와 같은 weight decay-like penalty term을 추가할 것입니다. (여기서 $\lambda$는 small rewards를 가지는 것과 (6)을 maximizing 하는 것 두 목표 사이를 balancing 할 수 있는 adjustable penalty coefficient입니다.)
최대한 쉽게 풀어서 다시 설명해 보겠습니다. 위의 수식 (6)으로 maximizing을 한다고 했을 때, Q값들에 대해서 보다 더 R를 simple하게 정하고, 수식 (6)을 더 maximizing이 잘 되도록 penalty term을 추가하는 것입니다. 쉽게 말해 우리가 Loss function에서 regularization term을 두는 것처럼 더 효과적이고 쉽게 사용하기 위해서 하는 작업이라고 생각하면 편합니다. $Q^\pi (s, a_1)$과 Q값들 사이가 더 극명하도록 L1 regularization term을 두어서 R를 쉽게 정하자!라는 것입니다.
이렇게 함으로써 "simplest" R (largest penalty coefficient)을 찾을 수 있고, R은 왜 $\pi$가 optimal 한 지를 "explain"할 수 있습니다. 정리하여 다시 optimization problem을 수식으로 말하자면 다음과 같습니다.
First objective function & algorithm
$$
maximize \sum_{i=1}^N \min_{a \in {a_2, ... , a_k}} \{(P_{a_1} (i) - P_a (i))(I - \gamma P_{a_1})^{-1} R\} - \lambda ||R||_1
$$
$$
s.t. (P_{a_1} - P_a)(I - \gamma P_{a_1})^{-1} R \succeq 0 \forall a \in A \setminus a_1
$$
$$
|R_i| \leq R_{max}, i = 1, ... , N
$$
이러한 수식들을 통해 linear program으로 표현될 수 있고, 효과적으로 해결될 수 있습니다.
4. Linear Function Approximation in Large State Spaces
이번 section에서는 infinite state spaces의 case를 다룹니다. infinite-state MDPs는 section 2에서의 finite-state와 같은 방식으로 정의될 수 있습니다. 추가적으로 state는 $S = \mathbb{R}^n$의 case에 대해서만 다루고자 합니다. 따라서 reward function R은 $S = \mathbb{R}^n$로부터의 function이라고 할 수 있습니다. Calculus of variations는 infinite state spaces에서 optimizing 하는 데에 있어 좋은 tool이지만, 종종 알고리즘적으로 어렵게 만듭니다. 따라서 reward function에 대해 "Linear Functional Approximation"을 사용합니다. 수식으로 R을 표현하자면 다음과 같습니다.
$$\begin{equation}
R(s)=\alpha_1 \phi_1(s)+\alpha_2 \phi_2(s)+\cdots+\alpha_d \phi_d(s)
\tag{8}\end{equation}$$
여기서 $\phi_1, ... , \phi_d$는 $S$로부터 mapping 된 고정되어 있고, 우리가 알고 있고, bound 되어 있는 basis function입니다. 그리고 $\alpha_i s$는 우리가 fit 해야 하는 알고 있지 않은 parameter입니다.
다음으로 $V^\pi$에 대해서도 linearity of expectation을 함으로써, reward function R이 Equation (8)로 주어질 때 value function을 다음과 같이 표현할 수 있습니다.
$$\begin{equation}
V^\pi=\alpha_1 V_1^\pi+\cdots+\alpha_d V_d^\pi
\tag{9}\end{equation}$$
위의 수식과 Theorem 2 (3번 수식)을 사용하면서, policy $\pi (s) \equiv a_1$를 optimal 하도록 만드는 R에 대해서 (4)의 appropriate generalization은 다음의 조건입니다.
$$\begin{equation}
\mathrm{E}_{s^{\prime} \sim P_{s a_1}}\left[V^\pi\left(s^{\prime}\right)\right] \geq \mathrm{E}_{s^{\prime} \sim P_{s a}}\left[V^\pi\left(s^{\prime}\right)\right]
\end{equation} \\ \text { for all states } s \text { and all actions } a \in A \backslash a_1 \tag{10} $$
하지만 위의 formulation들에는 두 가지 문제가 있습니다.
- infinite state spaces에서, Equation (10)의 형태에는 infinitely 많은 제약이 있습니다. infinite state spaces이기 때문에 모든 state를 check 하기가 불가능하고 어렵습니다. 따라서 알고리즘적으로, states 중의 finite subset $S_0$만 sampling 함으로써 이러한 문제를 피하고자 합니다.
- R을 표현하기 위해 Equation (8)에서 linear function approximator를 사용한다고 제한했기 때문에, 어느 $\pi$가 optimal 한 지에 대해 더 이상 어떠한 reward function도 표현할 수 없습니다. 그럼에도 불구하고, linear function approximator를 사용할 것입니다.
최종적으로 linear programming formulation은 다음과 같습니다.
Second objective function & algorithm
$$
\operatorname{maximize} \sum_{s \in S_0} \min _{a \in\left\{a_2, \ldots, a_k\right\}}\left\{ p\left(\mathrm{E}_{s^{\prime} \sim P_{s a_1}}\left[V^\pi\left(s^{\prime}\right)\right]-\mathrm{E}_{s^{\prime} \sim P_{s a}}\left[V^\pi\left(s^{\prime}\right)\right]\right)\right\}
$$
$$
s.t. |\alpha_i| \leq 1, i = 1, ... , d
$$
5. IRL from Sampled Trajectories
이번 section에서는 오직 state space에서의 actual trajectories의 set을 통해서만 policy $\pi$를 접근하는 좀 더 realistic case에 대해서 IRL 문제를 다룹니다. 그래서 MDP의 explicit model을 필요로 하지 않습니다. initial state distribution $D$를 고정하고, (unknown) policy $\pi$에 대해 우리의 목표는 $\pi$가 $\mathbb{E}_{s_0 \sim D} [V^\pi (s_0)]$를 maximize 하는 R를 찾는 것입니다. (기억합시다!) 추가적으로 notation을 단순화하기 위해 고정된 start state $s_0$를 가정합니다.
먼저 $\alpha_i$의 setting을 통해 $V^\pi (s_0)$를 estimating 하는 방법이 필요합니다. 이것을 하기 위해, 첫 번째로 $m$ Monte Carlo trajectories를 만들어냅니다. 그러고 나서 $i = 1, ... , d$ 에 대해 만약 reward가 $R = \phi_i$라면, $V_i^\pi (s_0)$를 얼마나 average empirical return이 $m$ trajectories에 있었는 지로 정의합니다. 예를 들어, 만약 $m = 1$ trajectories이고, 이 trajectory가 states ($s_0, s_1, ...$)의 sequence라면, 다음과 같이 나타낼 수 있습니다.
$$
\hat{V}_i^\pi (s_0) = \phi_i (s_0) + \gamma \phi_i (s_1) + \gamma^2 \phi_i (s_2) + \cdots
$$
일반적으로, $\hat{V}_i^\pi (s_0)$은 어떠한 $m$ trajectories의 empirical returns에 대하여 average 합니다. (여기서 말하는 어떠한 $m$ trajectories는 임의의 finite number에 의해 truncate 된 trajectories를 말합니다.) 그리고 그때 $\alpha_i$의 어떠한 setting에 대해서, $V^\pi (s_0)$의 natural estimate는 다음과 같습니다.
$$\begin{equation}
\hat{V}^\pi\left(s_0\right)=\alpha_1 \hat{V}_1^\pi\left(s_0\right)+\cdots+\alpha_d \hat{V}_d^\pi\left(s_0\right)
\tag{11}\end{equation}$$
위의 수식의 "inductive(귀납적인) step"은 다음을 뒤따릅니다 : set of policies ${ \pi_1, ... , \pi_k }$이 있고, resulting reward function은 아래의 수식을 만족하기 때문에 $\alpha_i$의 setting을 찾을 수 있습니다.
$$\begin{equation}
V^{\pi^*}\left(s_0\right) \geq V^{\pi_i}\left(s_0\right), \quad i=1, \ldots, k
\tag{12}\end{equation}$$
그리고 section 4에서 마지막에 있던 수식에서, objective function을 약간 바꿀 수 있습니다. 따라서 optimization의 식은 다음과 같이 될 수 있다.
Final objective function & algorithm
$$
maximize \sum_{i=1}^k p(\hat{V}^{\pi^*} (s_0) - \hat{V}^{\pi_i} (s_0))
$$
$$
s.t. |\alpha_i| \leq 1, i = 1, ... , d
$$
위의 수식에서 $\hat{V}^{\pi_i} (s_0)$과 $\hat{V}^{\pi^*} (s_0)$은 Equation (11)에서 주어진 $\alpha_i$의 (implicit) linear function이다.
그러므로, 위의 $\hat{V}^{\pi_i} (s_0)$과 $\hat{V}^{\pi^*} (s_0)$은 쉽게 linear programming으로 해결할 수 있습니다.
위의 optimization 식은 $\alpha_i$의 새로운 setting으로 설정할 수 있고, 그러므로 새로운 reward function $R = \alpha_1 \phi_1 + \cdots + \alpha_d \phi_d$을 가질 수 있습니다. 그리고 그때 $R$로 인한 $V^\pi (s_0)$를 maximize 하는 policy $\pi_{k+1}$을 찾을 수 있고, $\pi_{k+1}$을 current set of policies에 추가할 수 있습니다. 그리고 이것을 계속할 수 있습니다. (많은 수의 iteration을 통해 우리가 "satisfied"하는 $R$를 찾을 수 있습니다.)
6. Experiments
6.1 First experiment : 5 x 5 grid world
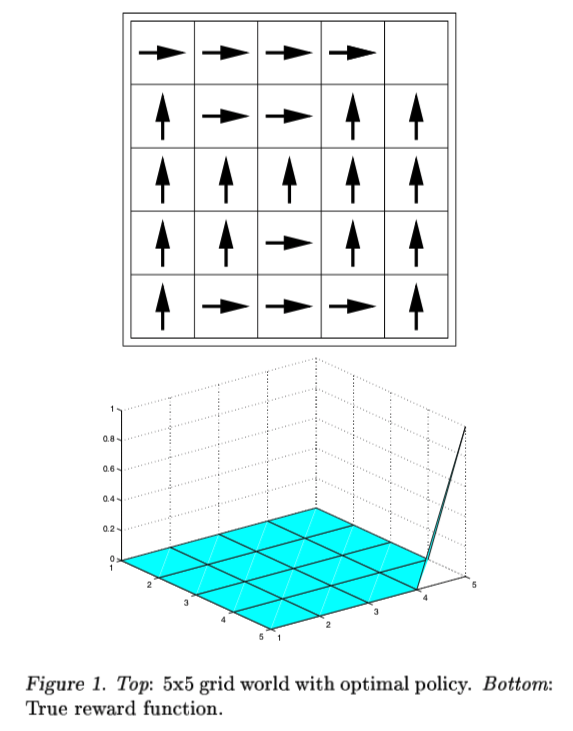
첫 번째 실험은 agent가 왼쪽 아래에서 시작하여 오른쪽 위로 가면 보상 1을 받는 5x5 grid world를 사용했습니다. action은 상하좌우지만 noise가 있으며 30%의 확률로 랜덤 하게 움직입니다. 위에 있는 Figure 1은 5x5 grid world에서의 optimal policy와 true reward function을 나타낸 것입니다.
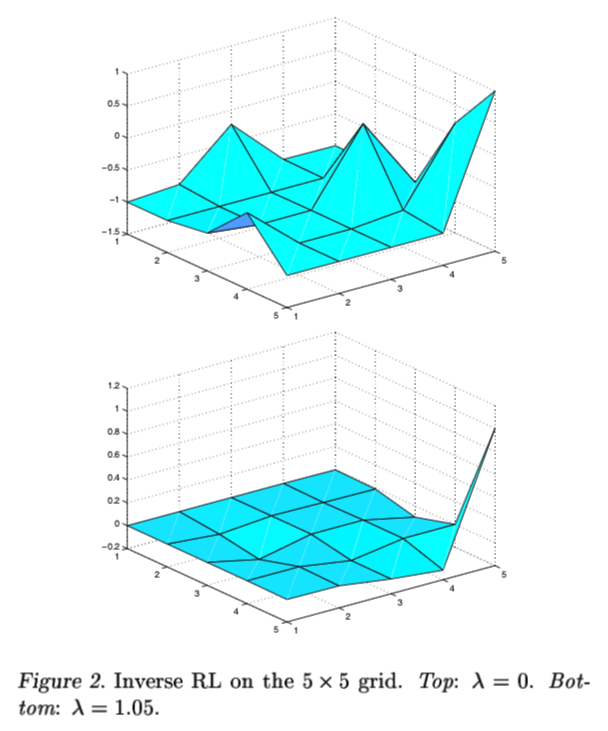
앞에서 설명한 penalty term인 $\lambda$를 주지 않은 Section 3.2의 discrete/finite state problem에서 사용할 수 있는 algorithm을 쓰면 Figure 2 윗부분의 그림과 같은 울퉁불퉁한 reward function의 모습을 볼 수 있습니다. 위에서 말했던 section 3.2에 있는 algorithm은 다음과 같습니다.
$$
maximize \sum_{i=1}^N \min_{a \in {a_2, ... , a_k}} \{(P_{a_1} (i) - P_a (i))(I - \gamma P_{a_1})^{-1} R\} - \lambda ||R||_1
$$
$$
s.t. (P_{a_1} - P_a)(I - \gamma P_{a_1})^{-1} R \succeq 0 \forall a \in A \setminus a_1
$$
$$
|R_i| \leq R_{max}, i = 1, ... , N
$$
그러나 Figure 2 아래에 쓰여 있는 $\lambda$ = 1.05로 설정을 하면 Figure 2 아래에 있는 그림과 같은 true reward에 밀접한 reward function을 얻을 수 있습니다.
6.2 Second experiment : Mountain-car

다음 실험으로는 보통 잘 알려져 있는 mountain-car 환경입니다. ture, undiscounted reward는 언덕에 있는 goal지점에 도달하기 전까지 step마다 -1을 받는 것입니다. 그리고 state는 자동차의 x-위치와 속도입니다.
$$
\operatorname{maximize} \sum_{s \in S_0} \min _{a \in\left\{a_2, \ldots, a_k\right\}}\left\{ p\left(\mathrm{E}_{s^{\prime} \sim P_{s a_1}}\left[V^\pi\left(s^{\prime}\right)\right]-\mathrm{E}_{s^{\prime} \sim P_{s a}}\left[V^\pi\left(s^{\prime}\right)\right]\right)\right\}
$$
$$
s.t. |\alpha_i| \leq 1, i = 1, ... , d
$$
state가 연속적이기 때문에 위의 수식과 같이 section 4의 continuous/finite state problem에서 사용할 수 있는 algorithm을 사용했습니다. 또한 reward에 대해서 오직 자동차의 x-위치에 대한 functions가 되도록 Gaussian 모양으로 된 26개의 basis functions의 linear combinations을 가지는 function approximator class를 구성하였습니다.

algorithm으로 optimal policy를 고려하여 전형적인 reward function은 Figure 4의 윗부분에 있는 그래프로 나타납니다. (Note the scale on the $y$ axis.) 명확하게도, solution은 reward의 $R = -c$ structure를 거의 완벽하게 나타내었습니다. 좀 더 challenging 한 문제로서, 이 논문에서는 언덕 아래 주변을 중심으로 [-0.72, -0.32] 사이에 있으면 reward 1 아니면 0을 주도록 changed ture reward에 대한 실험을 동일하게 하였습니다. 그리고 여기서 $\gamma$는 0.99를 주었다고 합니다.
이 문제에서의 optimal policy는 가능한 한 빨리 언덕 아래로 가서 주차를 하는 것입니다. 새로운 문제에 대해 알고리즘을 적용해 봤을 때 전형적인 solution은 Figure 4 아래에 있는 그래프로 나타낼 수 있습니다. 대체로 reward의 중요한 structure를 정해진 [-0.72, -0.32]에 대해 성공적으로 찾았다고 합니다. 또한 오른쪽에는 artifact가 있어 오른쪽 끝을 피할 수 없도록 "shooting out"하는 효과가 있다고 합니다. 그럼에도 불구하고, solution이 이 문제에 꽤 좋았다고 합니다.
6.3 Final experiment : Continuous version of the 5 x 5 grid world
마지막 실험은 5x5 grid world의 continuous version에서 적용했습니다. state는 [0, 1] x [0, 1]이고, action은 상하좌우 방향으로 0.2만큼 움직입니다. 또한 [-0.1, 0.1]의 uniform noise가 각각 좌표에 추가되고, 만약 unit square 내에 uniform noise가 필요한 경우, state는 truncate 됩니다. reward는 [0.8, 1] x [0.8, 1]에서는 1을 받고 나머지는 0을 받습니다. 그리고 $\gamma$는 0.9를 사용했습니다. 또한 function approximator class는 2-dimensional Gaussian basis functions에 대한 15x15 array의 linear combinations로 구성하였습니다. initial state distribution $D$는 state space에 대해 uniform 하였고, algorithm은 policy를 평가하기 위해 각각의 30 steps 마다 $m=5000$ trajectories를 사용하여 적용하였습니다.
$$
maximize \sum_{i=1}^k p(\hat{V}^{\pi^*} (s_0) - \hat{V}^{\pi_i} (s_0))
$$
$$
s.t. |\alpha_i| \leq 1, i = 1, ... , d
$$
위에서 다뤘던 section 5에서의 algorithm을 사용하여 찾아진 solution은 단지 1 iteration만 했는데도 꽤나 reasonable 했습니다. 그래서 약 15 iterations에 대해서도 해본 결과, algorithm은 동일하게 좋은 performance로 해결했습니다.
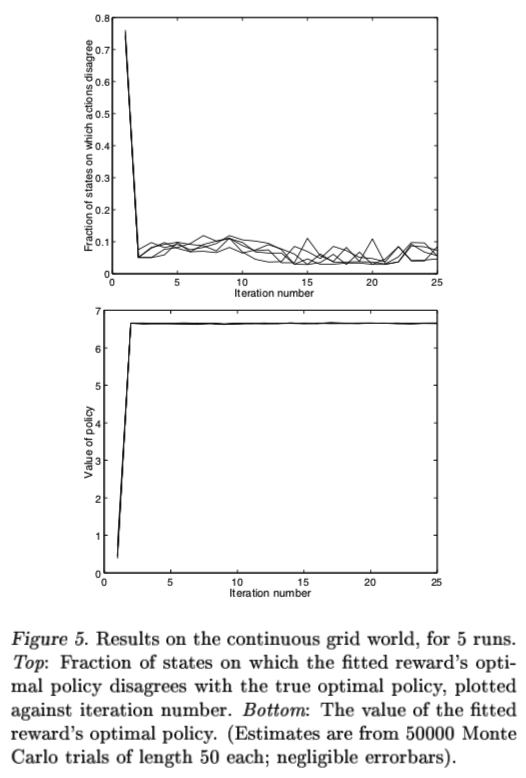
또한 action choice가 다른 state sapce의 부분을 계산하면서 true optimal policy와 fitted reward’s optimal policy를 비교하였고 (Figure 5, 위), 대체적으로 3% ~ 10% 사이로 불일치했습니다. 아마도 algorithm's performance의 좀 더 적절한 측정은 true optimal policy의 quality와 fitted reward’s optimal policy의 quality를 비교하는 것입니다. (Quality는 물론 true reward function을 사용하여 측정됩니다.) 결과적으로 algorithm의 약 15 iterations에 대해서, evaluations은 (which used 50000 Monte Carlo trials of 50 steps each) true "optimal policy"의 value와 fitted reward’s optimal policy사이에 statistically 한 중요한 차이를 detect 할 수 없다는 것을 볼 수 있었습니다. 그만큼 true optimal policy와 reward's optimal policy의 차이가 없다는 것을 뜻합니다. (Figure 5, 아래)
7. Conclusions and Future work
이 논문은 moderate-sized discrete and continuous domain에서 Inverse Reinforcement Learning 문제가 해결될 수 있다는 것을 보였습니다. 하지만 많은 open question들이 아래와 같이 남아있습니다.
- Potential-based shaping rewards는 MDP에서 학습시키기 위한 하나의 solution으로서 reward function을 더 쉽게 만들 수 있습니다. 그렇다면 우리는 더 "easy" reward function을 만들기 위한 IRL 알고리즘들을 만들 수 있을까요?
- IRL를 real-world empirical application측면에서 보면, sensor inputs and actions에 대해서 observer의 측정에 상당한 noise가 있을지도 모릅니다. 여기에 더하여 많은 optimal policy들이 존재할지도 모릅니다. 어떠한 data를 noise 없이 fit 하도록 하는 적절한 metric은 무엇일까요?
- 만약 행동이 절대로 optimality와 일치하지 않는다면, state space에 specific region에 대한 "locally consistent" reward function을 어떻게 알 수 있을까요?
- 어떻게 reward function의 identifiability를 maximize 하기 위한 실험을 고안해 낼 수 있을까요?
- 이 논문에 적힌 알고리즘적인 접근이 partially observable environment의 case를 얼마나 잘 실행할 수 있을까요?
'프로젝트 > GAIL 하자' 카테고리의 다른 글
| 6. Generative Adversarial Imitation Learning (0) | 2023.02.21 |
|---|---|
| 5. Maximum Entropy Inverse Reinforcement Learning (1) | 2023.02.21 |
| 4. Maximum Margin Planning (0) | 2023.02.20 |
| 3. Apprenticeship Learning via Inverse Reinforcement Learning (0) | 2023.02.19 |
| 1. Let's do Inverse RL Guide (1) | 2023.02.18 |
