
논문 저자 : Will Dabney, Georg Ostrovski, David Silver, Rémi Munos
논문 링크 : ArXiv
Proceeding : The 36th International Conference on Machine Learning (ICML 2018)
정리 : 민규식
Introduction
본 게시물은 2018년 6월에 발표된 논문 Implicit Quantile Networks for Distributional Reinforcement Learning 의 내용에 대해 설명합니다.

Algorithm
IQN의 경우 QR-DQN과 비교했을 때 크게 다음의 2가지 정도에서 차이를 보입니다.
- 동일한 확률로 나눈 Quantile을 이용하는 대신 확률들을 random sampling하고 해당하는 support를 도출
- 네트워크 구조
위의 내용들에 대해 하나하나 살펴보도록 하겠습니다.
1. Sampling
QR-DQN vs IQN
QR-DQN 논문에서는 quantile regression 기법을 이용하여 Wasserstein distance를 줄이는 방향으로 분포를 학습하였고 이에 따라 distributional RL의 수렴성을 증명하였습니다. 이에 따라 IQN 논문에서도 quantile regression 기법을 그대로 이용합니다. 심지어 QR-DQN 논문에서 사용한 Quantile huber loss도 그대로 사용합니다. Target network, experience replay, epsilon-greedy도 QR-DQN과 동일하게 사용합니다. 하지만 IQN에서는 Cumulative Distribution Function을 동일한 확률로 나누는 대신 random sampling을 통해 취득한 tau에 해당하는 support를 도출합니다.
예를 들어보겠습니다. Quantile의 수를 4라고 해보겠습니다. 이 경우 QR-DQN의 quantile값은 [0.25, 0.5, 0.75, 1]이지만 QR-DQN은 Wasserstein distance를 최소로 하기 위해 quantile의 중앙값에 해당하는 support를 도출합니다. 즉 [0.125, 0.375, 0.625, 0.875]에 해당하는 support들을 추정합니다.
하지만 IQN 논문에서는 quantile값 tau를 0~1 사이에서 임의로 sampling합니다. Quantile이 4개인 경우 랜덤하게 추출한 0~1사이의 4개의 값이 [0.12, 0.32, 0.78, 0.92] 라고 해보겠습니다.
위의 예시를 그림으로 표현한 것이 아래와 같습니다.

해당 내용에 대해서는 논문에서 나타낸 그림이 굉장히 잘 표현하고 있습니다. 이 그림의 경우 DQN, C51, QR-DQN, IQN의 경우를 아래와 같이 모두 비교하고 있습니다.

다들 network 구조에도 차이가 존재하지만 일단은 output만을 비교해보도록 하겠습니다.
- DQN: 각 action에 대한 value
- C51: 각 action에 대한 value distribution 중 확률 (support는 고정값으로 사용)
- QR-DQN: 각 action에 대한 value distribution 중 support (확률은 고정값으로 사용)
- IQN: 각 action에 대한 value distribution 중 support (확률은 random sampling)
그럼 이렇게 sampling을 한 tau를 통해 support를 추정하는 것은 어떤 좋은 점이 있을까요? 논문에 따르면 Risk-Sensitive하게 Policy를 선택할 수 있습니다. 해당 내용에 대해 한번 살펴보도록 하겠습니다.
Risk-Sensitive Reinforcement Learning
일단은 여기서 말하는 Risk가 무엇을 의미하는지 먼저 알아보도록 하겠습니다.
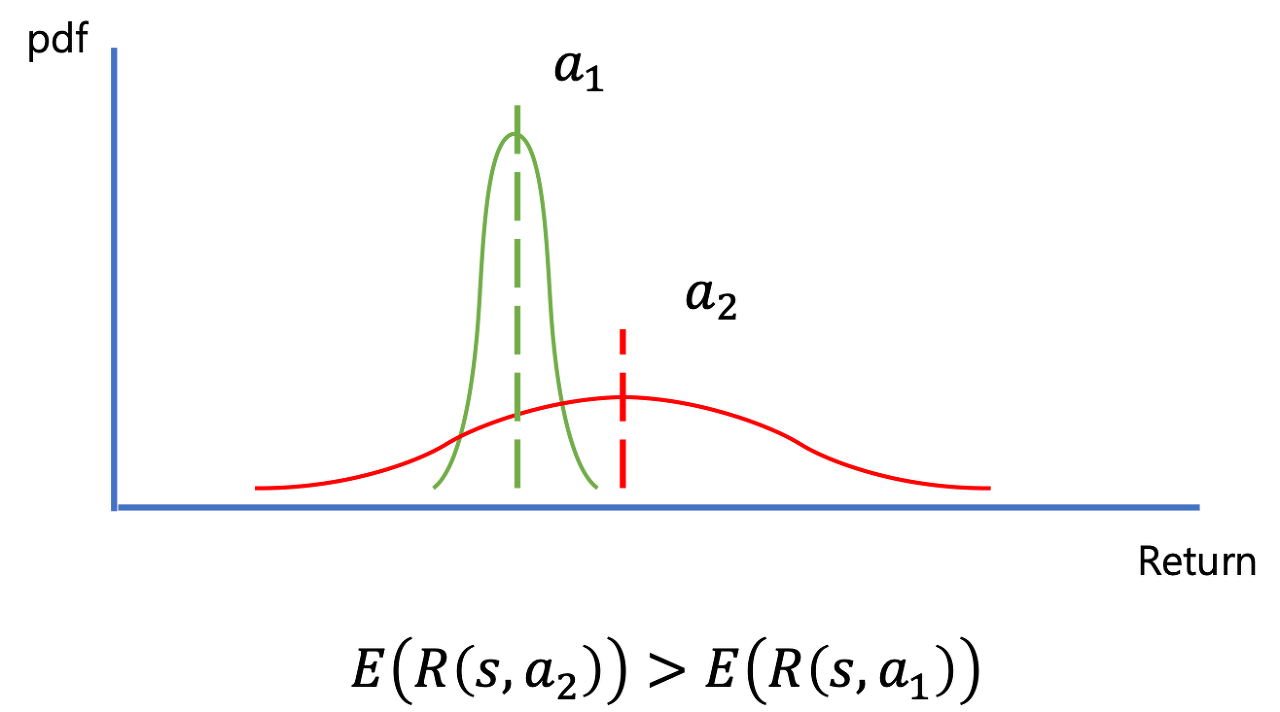
위의 그림을 보시면 2개의 action에 대한 value distribution이 각각 존재합니다. Action 1 (a1)에 대한 distribution은 분산이 작기 때문에 평균값에 가까운 return을 받을 확률이 높습니다. 하지만 value distribution의 기대값이 action2 (a2)보다 작습니다. Distributional RL에서는 distribution의 기대값을 비교하여 action을 선택하기 때문에 이런 경우 a2가 선택될 것입니다.
a2의 경우 분산이 매우 큰 distribution입니다. 이런 분포에서는 경우에 따라 매우 작은 return이 도출될 수도 있고, 매우 높은 return이 도출될수도 있습니다. Distributional RL에서는 이렇게 분산이 커서 결과에 대한 확신이 낮은 경우 “Risk가 크다”고 합니다. 반대로 결과에 대한 확신이 상대적으로 높은 a1의 경우 a2에 비해 “Risk가 작다”라고 할 수 있는 것이죠.
Sampling을 통해 학습을 수행하고 action을 선택하는 경우 이 risk에 따라 action을 선택하는 것이 가능합니다. 이런 risk sensitive policy에는 다음의 2가지가 있습니다.
- Risk-averse policy
- Risk-seeking policy
A Comprehensive Survey on Safe Reinforcement Learning 논문을 보시면 다음과 같은 내용이 나옵니다.

위의 definition을 보시면 scalar parameter beta를 통해 risk의 level을 결정합니다. 이 beta를 risk sensitivity parameter라고 합니다. 이 beta가 0보다 큰 경우 risk-averse, 0보다 작은 경우 risk-seeking, 그리고 0인 경우 risk-neutral policy가 됩니다.
어떻게 beta를 통해 risk의 level을 결정할 수 있는지, sampling을 이용하면 어떻게 risk-sensitive policy를 결정할 수 있는지 한번 알아보겠습니다.
우선 risk-sensitive policy에 따라 action을 선택하는 식은 다음과 같습니다.


위의 경우는 RIsk-averse 입니다. 기존의 경우 a2의 distribution에 대한 평균값이 a1의 distribution에 대한 평균값보다 크기 때문에 a2를 최종적인 action으로 선택했을 것입니다. 하지만 a1보다 a2의 분산이 훨씬 크기 때문에 beta가 양수인 경우 (distribution의 평균) - beta * (distribution의 분산)의 계산을 수행하면 연산의 결과값은 a2보다 a1이 더 큽니다. 이에 따라 risk가 더 낮은 a1을 선택하게 되는 것이고 위와 같은 과정을 통해 risk-averse policy에 따라 action을 선택하게 됩니다.
CDF의 낮은 영역에서만 tau를 sampling하는 경우 위와 유사한 결과를 확인할 수 있습니다. Tau를 낮은 범위 내에서 sampling하는 경우 낮은 value들에 대한 tau들이 sampling되지만 a2의 경우 a1보다 분산이 훨씬 크기 때문에 sampling 된 결과들의 기대값은 a1이 a2보다 크게 됩니다.
Risk-seeking의 경우 위의 risk-averse와 반대의 상황을 확인할 수 있습니다.

위의 경우는 RIsk-seeking 입니다. 기존의 경우 a1의 distribution에 대한 평균값이 a2의 distribution에 대한 평균값보다 크기 때문에 a1를 최종적인 action으로 선택했을 것입니다. 하지만 a1보다 a2의 분산이 훨씬 크기 때문에 beta가 음수인 경우 (distribution의 평균) - beta * (distribution의 분산)의 계산을 수행하면 연산의 결과값은 a1보다 a2가 더 큽니다. 이에 따라 risk가 더 큰 a2를 선택하게 되는 것이고 위와 같은 과정을 통해 risk-seeking policy에 따라 action을 선택하게 됩니다.
CDF의 높은 영역에서만 tau를 sampling하는 경우 위와 유사한 결과를 확인할 수 있습니다. Tau를 높은 범위 내에서 sampling하는 경우 높은 value들에 대한 tau들이 sampling되지만 a2의 경우 a1보다 분산이 훨씬 크기 때문에 sampling 된 결과들의 기대값은 a2가 a1보다 크게 됩니다.
논문에서는 다음과 같은 4가지 기법들을 이용해 tau를 위한 sampling distribution을 변경하고 다양한 risk-sensitive policy를 선택하게 됩니다.
- Cumulative Probability Weighting (CPW)
- Wang
- Power formula (POW)
- Conditional Value-at-Risk (CVaR)
위의 예시 중에 가장 간단한 CVaR에 대해서 살펴보도록 하겠습니다. CVaR의 수식은 다음과 같습니다.

원래 tau는 [0,1] 중에서 uniform한 확률로 선택합니다. 하지만 위의 경우 eta를 예를 들어 0.25로 하면 0.25tau가 됩니다. 즉 [0, 0.25] 중에서 uniform한 확률로 tau를 sampling하게 됩니다. 결과적으로 risk-averse policy에 따라 action을 선택하게 됩니다.
2. Network
여기서는 IQN 네트워크의 구조에 대해 살펴보도록 하겠습니다. 일단 위에서 봤던 그림을 다시 한번 살펴보도록 하겠습니다.

위의 그림에서 DQN과 IQN만 비교해보도록 하겠습니다.
특정 action a에 대해 DQN은 다음과 같은 함수들로 나타낼 수 있습니다.

위의 식에서 psi는 convolution layers에 의한 연산을, f는 fully-connected layers에 의한 연산을 나타냅니다.
IQN도 DQN과 동일한 function인 psi와 f를 이용합니다. 그 대신 거기에 tau를 embedding 해주는 함수 phi를 추가적으로 사용합니다. 이에 따라 특정 action a에 대해 IQN을 함수로 나타낸 것이 다음과 같습니다.

위의 식을 살펴보자면 convolution function (psi)를 통해 얻은 결과와 tau에 대한 embedding function (phi)를 통해 얻은 결과를 element-wise하게 곱해줍니다. 그리고 그 결과에 fully-connected layer 연산을 수행하여 최종적으로 action a에 대한 value distribution을 얻습니다.
즉 위의 그림에서도 볼 수 있듯이 tau를 embedding하는 function인 phi를 제외하고는 모두 DQN과 같다고 할 수 있습니다. 이에 따라 embedding function (phi)에 대해서 한번 살펴보도록 하겠습니다. 이 함수의 역할은 하나의 sampling된 tau를 벡터로 embedding 해주는 것입니다. 본 논문에서 embedding에 대한 function은 다음과 같은 n cosine basis function 입니다.

위의 식에서 n은 embedding dimension이며 값은 64로 설정하였습니다. tau는 sampling된 값이며 w와 b는 linear layer 연산을 위한 weight와 bias입니다. 위 수식만을 봐서는 embedding을 어떻게 수행할지 감이 오지 않을 수 있습니다! 하나의 quantile에 대해 어떻게 sampling을 하는지 그림과 함께 예를 들어보도록 하겠습니다.
1. 우선 0~1 사이의 서로 다른 값을 [batch size x 1]의 사이즈로 random sampling 합니다. 이 값들은 각각의 tau값을 나타냅니다.

2. [Batch size x 1]로 sampling한 tau들을 복제하여 embedding dimension 만큼 쌓아줍니다. 본 논문의 경우 embedding dimension은 64입니다. 위 과정에 대한 결과의 사이즈는 [batch size x embedding dim]이 됩니다.

3. 모든 [batch size x embedding dim]의 모든 row에 0 ~ (n-1) 을 1씩 증가시킨 값을 곱해줍니다. 그리고 모든 값에 pi를 곱해줍니다. 이렇게 계산한 결과의 dimension은 여전히 [batch size x embedding dim] 입니다.

4. 다음으로는 3의 결과에 cos 연산을 해주고 weight를 곱하고 bias를 더해줍니다. 그리고 해당 결과에 최종적으로 ReLU 함수를 적용해줍니다. 여기서 weight의 사이즈는 [embedding dim x convolution 결과의 크기] 이며 bias의 사이즈는 [convolution 결과의 크기] 입니다. 결국 embedding 연산의 최종 결과는 [batch size x convolution 결과의 크기]가 됩니다. Convolution 연산의 최종 결과 또한 크기가 [batch size x convolution 결과의 크기] 입니다. 이에 따라 둘은 크기가 같아지게 되고 이에 따라 element-wise 하게 곱할 수 있게 됩니다.

여기까지가 Embedding function의 내용입니다!
여기서 약간의 의문이 들 수 있을 것이라 생각합니다. 왜 n cosine basis function을 이용할까요? 논문에서는 다양한 함수에 대해서 실험을 수행하였고 그 결과 n cosine basis function이 가장 좋은 결과를 보였다고 합니다. 여러 함수에 대해 테스트한 결과는 다음과 같습니다.

3. Quantile Huber Loss
사실 본 논문에서는 QR-DQN에서 사용했던 Quantile Huber Loss를 그대로 이용합니다. 하지만 본 논문에서는 식을 다음과 같이 표시합니다.

본 논문에서 N은 추정을 위해 일반 network 연산에서 sampling한 tau의 수 입니다. N’은 target distribution 도출을 위해 target network 연산에서 sampling한 tau의 수 입니다. 위 식에 대해서는 QR-DQN에서 자세히 설명하였으므로 추가적인 설명은 하지 않도록 하겠습니다. 다만 본 논문에서는 N과 N’를 다양하게 바꿔가면서 테스트한 결과를 다음과 같이 보여줍니다.

위의 결과는 6개의 atari game에 대한 human-normalized agent performance의 평균을 나타냅니다. 왼쪽의 경우 초반 10M frame을 학습하였을 때 결과이며 오른쪽의 경우 마지막 10M frame의 학습 결과입니다. 다른 알고리즘의 경우 각각 왼쪽과 오른쪽에 대한 결과가 다음과 같습니다.
- DQN: (32, 253)
- QR-DQN: (144, 1243)
4. Action 선택
본 논문에서 action을 선택하는 식이 QR-DQN과 비교했을 때 약간의 차이가 있습니다. 해당 식은 다음과 같습니다.
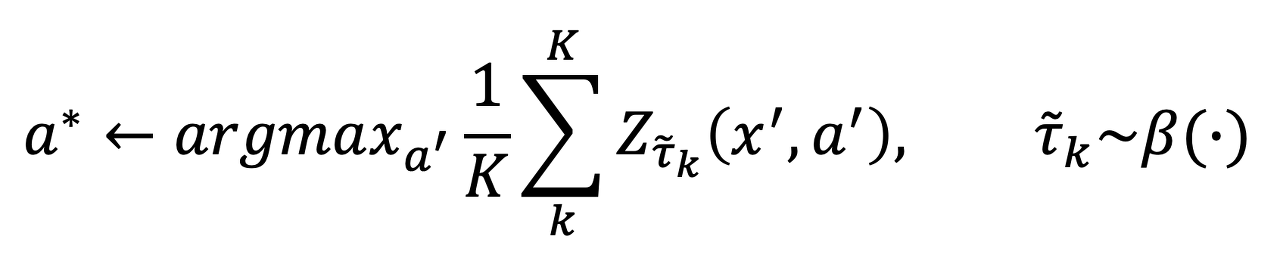
위 식은 단순히 sampling된 quantile을 통해 구한 모든 support의 값을 평균한 것입니다.
본 논문의 알고리즘은 다음과 같습니다.

Result
본 알고리즘의 성능은 Atari-57 benchmark를 통해 검증되었습니다.
본 알고리즘에서 설정한 파라미터 값은 다음과 같습니다.
Risk Sensitive Policy
우선 Risk의 정도를 다양하게 한 결과가 아래와 같습니다.

위의 결과에서 보면 CPW(.71)과 Norm(3)의 경우 distribution의 양 끝부분에 대한 영향을 감소시킵니다. Wang(.75)의 경우 Risk-seeking, Wang(-.75), Pow(-2), CVaR(.25) 그리고 CVaR(.1)의 경우 Risk-averse 한 policy를 선택합니다.
위의 결과를 비교해보면 다음과 같은 순서대로 우수한 성능을 보입니다.
Risk-averse > Neutral > Risk-seeking
이에 대해서는 대부분의 게임이 오래 살아있을 수록 받는 reward가 증가하기 때문에 불확실하면서 높은 reward를 선택하는 risk-seeking policy보다 작더라도 안정적인 reward를 선택하는 risk-averse policy가 좋은 성능을 보이는 것이라 생각할 수 있습니다.
Atari-57 Result
IQN 알고리즘을 57개의 Atari game에 테스트한 결과가 다음과 같습니다.

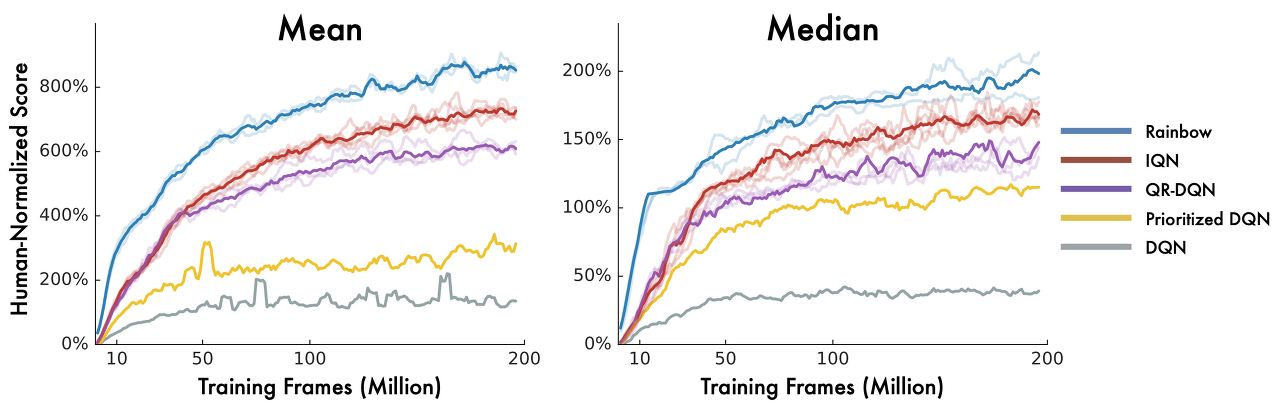
위의 결과에서 볼 수 있듯이 IQN은 단일 알고리즘임에도 불구하고 여러가지 기법을 조합한 Rainbow에 약간 못미치는 성능을 보입니다. 하지만 다른 단일 알고리즘인 Prioritized experience replay, C51, QR-DQN에 비해서는 모두 우수한 성능을 보이고 있습니다. 특히 QR-DQN에 비해 많은 변화가 없음에도 불구하고 기존의 단일 알고리즘 중 가장 좋은 성능을 보였던 QR-DQN보다 월등히 우수한 성능을 보이고 있습니다.
Robustness Test
다음의 결과는 같이 작업을 수행한 윤승제님께서 테스트해주신 결과입니다. Cartpole을 기본 파라미터로 학습을 수행한 후 Pole의 길이와 Pole의 질량을 다양하게 변경해가면서 테스트를 수행하였습니다. 알고리즘은 DQN과 IQN의 결과를 비교하였습니다.

까맣게 될수록 500점을 내지 못하고 중간에 떨어진 것입니다. 위의 결과에서 볼 수 있듯이 DQN은 파라미터의 변화에 취약하여 값을 변경하는 것에 따라 성능이 크게 저하되는 것을 확인할 수 있었습니다. 하지만 IQN의 경우 파라미터 변화에 매우 robust하여 parameter가 변해도 대부분의 경우 500점을 얻는 것을 확인할 수 있었습니다.
Conclusion
IQN은 QR-DQN에 비해 다음의 사항들만 변경해줬음에도 불구하고 훨씬 뛰어난 성능을 보이는 알고리즘입니다.
- Quantile을 random sampling하고 그때의 support를 도출하여 value distribution 취득
- Random sampling을 이용하여 risk-sensitive policy에 따른 action 선택 가능
- Network의 구조 변화 (DQN과 동일하나 convolution 연산의 결과를 embedding function 결과와 element-wise하게 곱해줌)
IQN의 경우 다양한 deep reinforcement learning 알고리즘들에 비해 좋은 성능을 보였으며 특히 단일 알고리즘임에도 불구하고 여러 알고리즘의 결합체인 Rainbow에 약간 못미치는 성능을 보였습니다. 또한 quantile regression을 이용하여 wasserstein distance를 줄이는 만큼 distributional RL의 수렴성을 증명했다는 QR-DQN의 장점은 그대로 가지고 있는 알고리즘이라 할 수 있습니다.
IQN을 끝으로 Deepmind에서 현재까지 (2018.11.01) 발표한 distributional RL에 대한 논문들에 대한 리뷰를 마치도록 하겠습니다!! 감사합니다!!
Implementation
본 논문의 코드는 다음의 Github를 참고해주세요.
GitHub - reinforcement-learning-kr/distributional_rl: Repository for studying distributional rl
Repository for studying distributional rl. Contribute to reinforcement-learning-kr/distributional_rl development by creating an account on GitHub.
github.com
Other Posts
Reference
Team
'프로젝트 > Distributional RL' 카테고리의 다른 글
| 3. Distributional Reinforcement Learning with Quantile Regression (0) | 2023.02.19 |
|---|---|
| 2. A Distributional Perspective on Reinforcement Learning (0) | 2023.02.19 |
| 1. Introduction to Distributional RL (0) | 2023.02.19 |
